But the equation for a parabola can also be written in "vertex form" y = a ( x − h) 2 k In this equation, the vertex of the parabola is the point ( h, k) You can see how this relates to the standard equation by multiplying it out y = a ( x − h) ( x − h) k y = a x 2 − 2 a h x a h 2 k This means that in the standard form, yGraph y=x^22x8 y = x2 − 2x − 8 y = x 2 2 x 8 Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Complete the square for x 2 − 2 x − 8 x 2 2 x 8 Tap for more steps Use the form a x 2 b x c a x 2 b x c, to find the values of a a, b b, and c cDivide 2, the coefficient of the x term, by 2 to get 1 Then add the square of 1 to both sides of the equation This step makes the left hand side of the equation a perfect square Add y3 to 1 Factor x^ {2}2x1 In general, when x^ {2}bxc is a perfect square, it can always be factored as \left (x\frac {b} {2}\right)^ {2}

Y X
Y=x^2-2x+8 vertex form
Y=x^2-2x+8 vertex form-Standard form quadratic equation in vertex form Converting by Finding the Vertex 1 Find the xvalue of the vertex by using 2 Input the xvalue of the vertex back into the quadratic to find the yvalue of the vertex 3 Input the vertex into the h and k values of the vertex form, which is y = a(x Convert to vertex form by completing the square 1 y = x 2 4x 2 y = x 2 2x 5 3 y = x 2 14x 59 4 y = 2x 2 36x 170
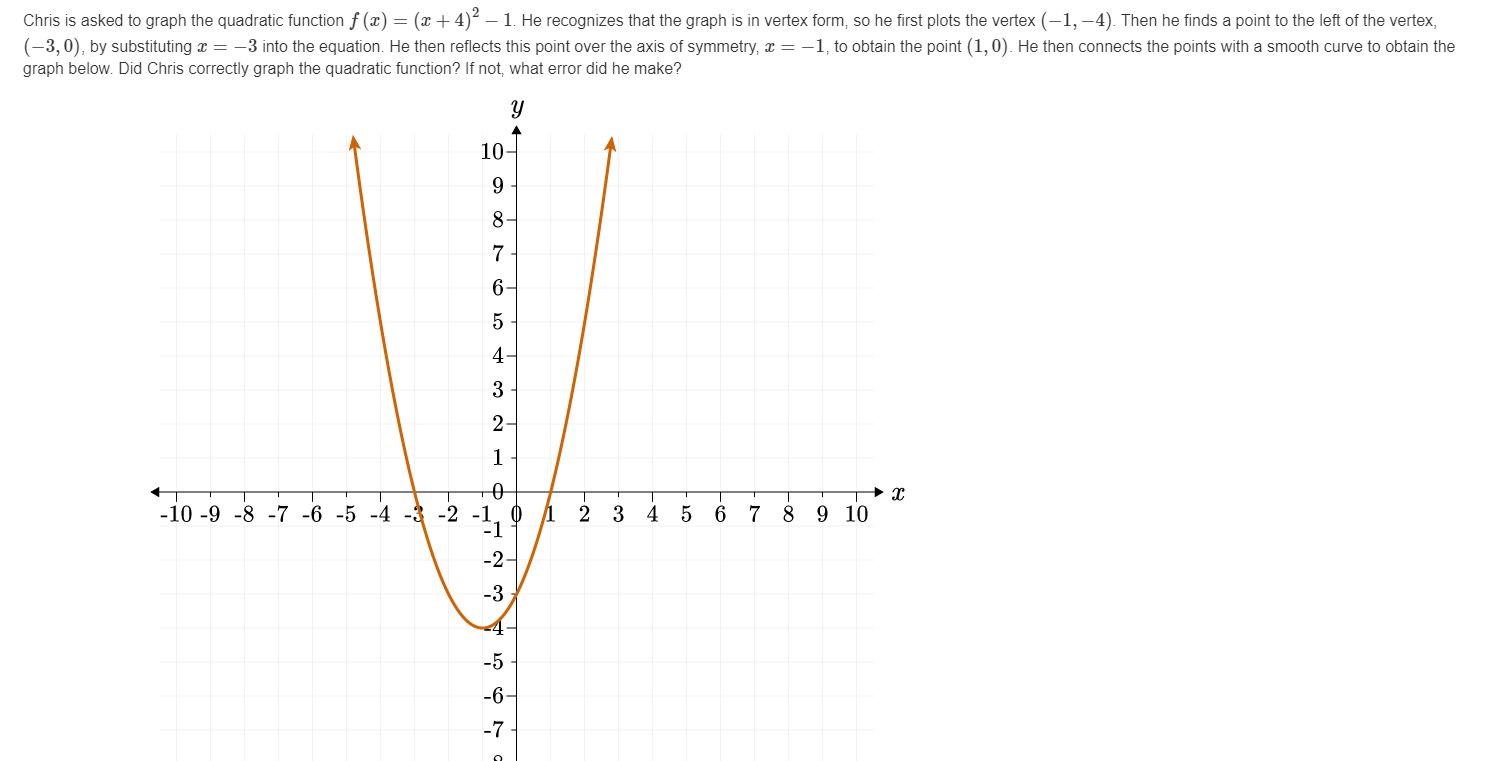



Chris Is Asked To Graph The Quadratic Function F X Chegg Com
How do I Change y=x^22x8 into factored form and then use the zero product property to find the x intercepts? To change the expression (x2 2x) into a perfect square trinomial add (half the x coefficient)² to each side of the expression Here x coefficient = 2 So, (half the x coefficient)2 = (2/2)2 = 1 Add and subtract 1 to the expression The vertex form of the parabola with vertex (h, k) and axis of symmetry x = h is y = a (x h)2 kFind the Vertex Form y=x^26x8 Complete the square for Tap for more steps Use the form , to find the values of , , and Consider the vertex form of a parabola Substitute the values of and into the formula Simplify the right side Tap for more steps Cancel the common factor of and
Solved by pluggable solver Completing the Square to Get a Quadratic into Vertex Form Start with the given equation Subtract from both sides Factor out the leading coefficient Take half of the x coefficient to get (ie ) Now square to get (ie ) Now add andHow do I find the vertex and the equation of the line of symmetry and graph?Divide 22\sqrt {y} by 2 The equation is now solved Swap sides so that all variable terms are on the left hand side Factor x^ {2}2x1 In general, when x^ {2}bxc is a perfect square, it can always be factored as \left (x\frac {b} {2}\right)^ {2} Take the square root of
Vertex Form Equation & Functions Just as y = mx b is a useful format for graphing linear functions, y = a(x h)^2 k is a useful format for graphing quadratic functionsThe vertex has an xvalue of b/2a=(16)/2=8 f(8)= 1 Therefore, the vertex is at (8,1) The vertex form is (xh)^2 k, where you change the sign of the x value of the vertex (h) and keep the y component (k) y=(x8)^2 1 Expand that for x^216x641 x^216x63Give the vertex of each function, and graph it How does vertex form compare to the other forms in each problem?




17 Transform Quadratic Functi See How To Solve It At Qanda



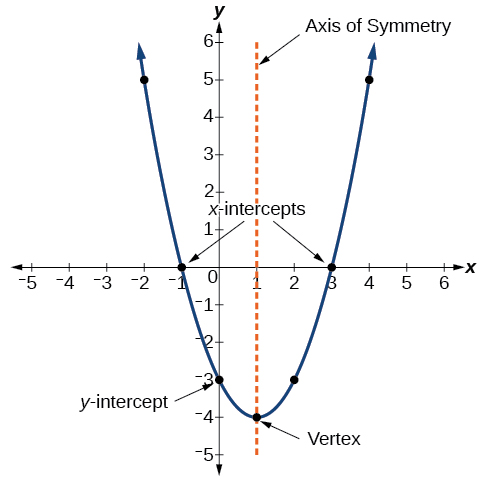
Axis Of Symmetry
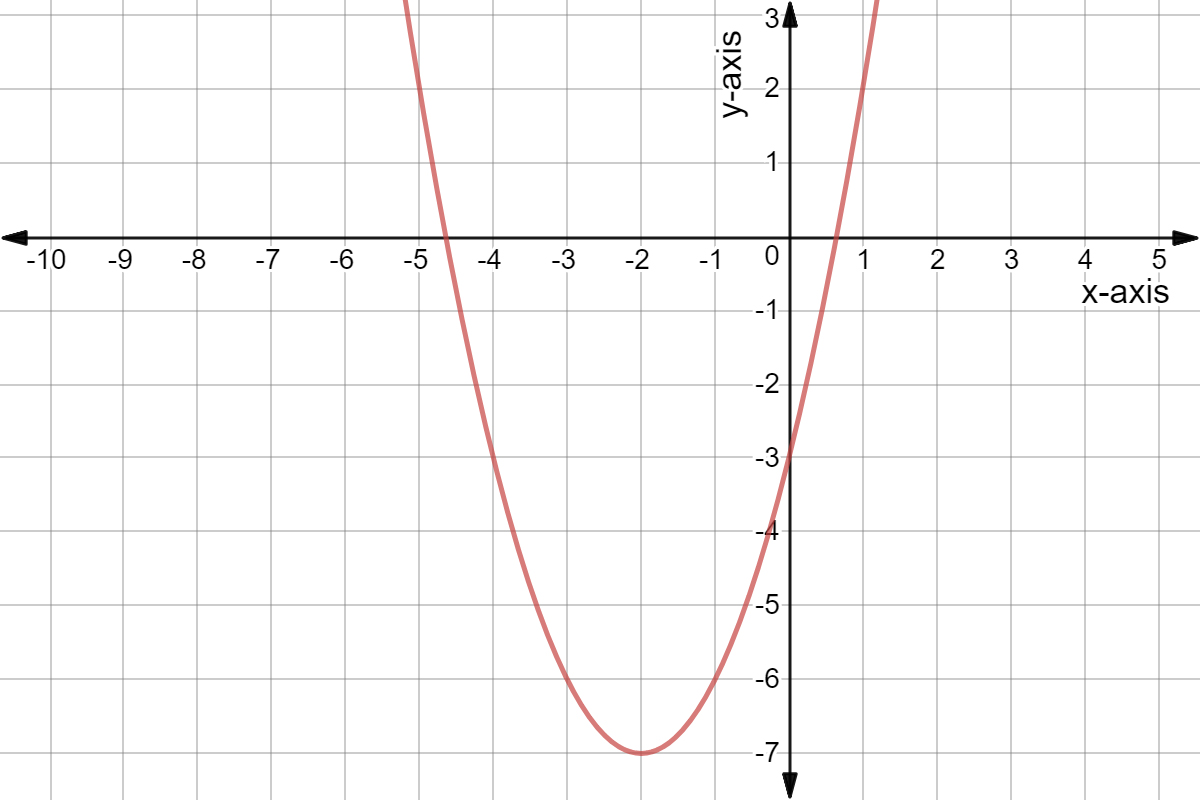
Question For the quadratic function f(x) = x^2 2x 8 Find a THe axis of symmetry and the vertex b THe xintercepts and y intercepts c The domain and range d Does the function have a maximum or minimum valueSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreParabola, Finding the Vertex 21 Find the Vertex of y = x 22x8 Parabolas have a highest or a lowest point called the Vertex Our parabola opens up and accordingly has a lowest point (AKA absolute minimum) We know this even before plotting "y" because the coefficient of the first term, 1 , is positive (greater than zero)



Biomath Quadratic Functions




Chapter 5 Study Guide
The equation in vertex form is , y=(x4)^21 The equation in vertex form is, y=x^28x15= (x4)^ =(x4)^21 Vertex is at (4,1) graph{x^28x15 10, 10,What Is The Axis Of Symmetry And Vertex For The Graph F X X 2 2x 8 Socratic For more information and source, Solution 3 The Graph Of Y X 2 2x 8 Intersects The X Axis At 1 2 And 4 2 2 And 4 3 2 And 4 4 2 And 4 Please Show Steps For more information and source,Learn to complete the square in order to write quadratic equations in vertex form Click Create Assignment to assign this modality to your LMS We have a new and improved read on this topic



Www Scasd Org Cms Lib Pa Centricity Domain 1229 2 2 a2 17 unit 2 2 ws packet lg Pdf




Exercises 2 3 In Problems 1 8 Find The Vertex Form Of Chegg Com
Problem y= x^24x6Complete the square with the x terms x^24x4 = y64 (x2)^2 = y2 ===== This shows you the vertex is at (2,2) and p= 1/4 ===== Cheers, Stan H Answer by jim_thompson5910() (ShowAnswer to Find the root of an equation y=x^22x8 By signing up, you'll get thousands of stepbystep solutions to your homework questionsDivide 0 0 by − 8 8 Multiply − 1 1 by 0 0 Add 8 8 and 0 0 Substitute the values of a a, d d, and e e into the vertex form a ( x d) 2 e a ( x d) 2 e Set y y equal to the new right side Use the vertex form, y = a(x−h)2 k y = a ( x h) 2 k, to determine the values of a a, h h, and k k



Practice 1 2 Graphing In Vertex Form And Intercept Form




Quadratic Equations And Quadratic Functions On The Sat
A) y = 2x 2 12x 16 B) y = 2x (x 6) 16 C) y = 2 (x 3) 2 (2) D) y = (x 2) (2x 8) Answer If you know the vertex form of an equation y = a (x h) 2 k then you will notice that only answer C is in that form Go to next Question Try the free Mathway calculator and problem solver below to practice various math topicsThe vertex form is a special form of a quadratic function From the vertex form, it is easily visible where the maximum or minimum point (the vertex) of the parabola is The number in brackets gives (trouble spot up to the sign!) the xcoordinate of the vertex, the number at the end of the form gives the ycoordinate36 is the value for 'c' that we found to make the right hand side a perfect square trinomial;



Ppt Building Understanding For Quadratics Powerpoint Presentation Free Download Id



Http Www Manhassetschools Org Cms Lib8 Ny Centricity Domain 710 Group work 59 63 solutions Pdf
Find the vertex y = 2x2 6 Technically, this is in standard form, but understanding that it could be written, y = 2(x 0)2 6, you can find the vertex using vertex form Find the vertex Best Answer If the equation has the form y = ax 2 bx c, the xcoordinate of the vertex is x = b/(2a) For the problem y = x 2 2x 8, a = 1, b = 2, and c = 8, so, the xcoordinate of the vertex is x = 2/2 or 111) y = (x 3)2 2 12) y = (x 4)2 13) y = x2 3 14) y = x2 3 Convert each function to standard form Give the vertex and yintercept



Vertex Form Of Quadratic Functions Math 2 Y




Find Factored Form And Vertex Of F X X 2 2x 8 Youtube
Y X 2 2x 8 Parabola Solution For The Quadratic Function F X X 2 2x 8 Find A The Axis Of Symmetry And The Vertex B The X Intercepts And Y Intercepts C The Domain And Range D For more information and source, see on this link httpsF(x)=1/8 x^2 How do i write an equation in standard form when given the point (7,3) and y intercept 2 asked Nov 19,Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more




What Is The Vertex Form Of Y X 2 16x 71 With Steps Please Brainly Com
%5E%7B2%7D%5C%20+%5C%2012%5C%5C%5Cvspace*%7B9%5Chspace*%7B-10%7D%7D%5C%5C&=&%5C%20-2(x%5C%20-%5C%208)(x%5C%20-%5C%208)%5C%20+%5C%2012%5C%5C%5Cvspace*%7B9%5Chspace*%7B-10%7D%7D%5C%5C&=&%5C%20-2%5Cleft%5B(x)(x)%5C%20+%5C%20(x)(-8)%5C%20+%5C%20(-8)(x)%5C%20+%5C%20(-8)(-8)%5Cright%5D%5C%20+%5C%2012%5C%5C%5Cvspace*%7B9%5Chspace*%7B-10%7D%7D%5C%5C&=&%5C%20-2(x%5E%7B2%7D%5C%20-%5C%208x%5C%20-%5C%208x%5C%20+%5C%2064)%5C%20+%5C%2012%5C%5C%5Cvspace*%7B9%5Chspace*%7B-10%7D%7D%5C%5C&=&%5C%20-2(x%5E%7B2%7D%5C%20-%5C%2016x%5C%20+%5C%2064)%5C%20+%5C%2012%5C%5C%5Cvspace*%7B9%5Chspace*%7B-10%7D%7D%5C%5C&=&%5C%20-2x%5E%7B2%7D%5C%20+%5C%2032x%5C%20-%5C%20128%5C%20+%5C%2012%5C%5C%5Cvspace*%7B9%5Chspace*%7B-10%7D%7D%5C%5C&=&%5C%20-2x%5E%7B2%7D%5C%20+%5C%2032x%5C%20-%5C%20116%5Cend%7Beqnarray%7D)



Characteristics Of Quadratic Functions Math 1 Eoct Review
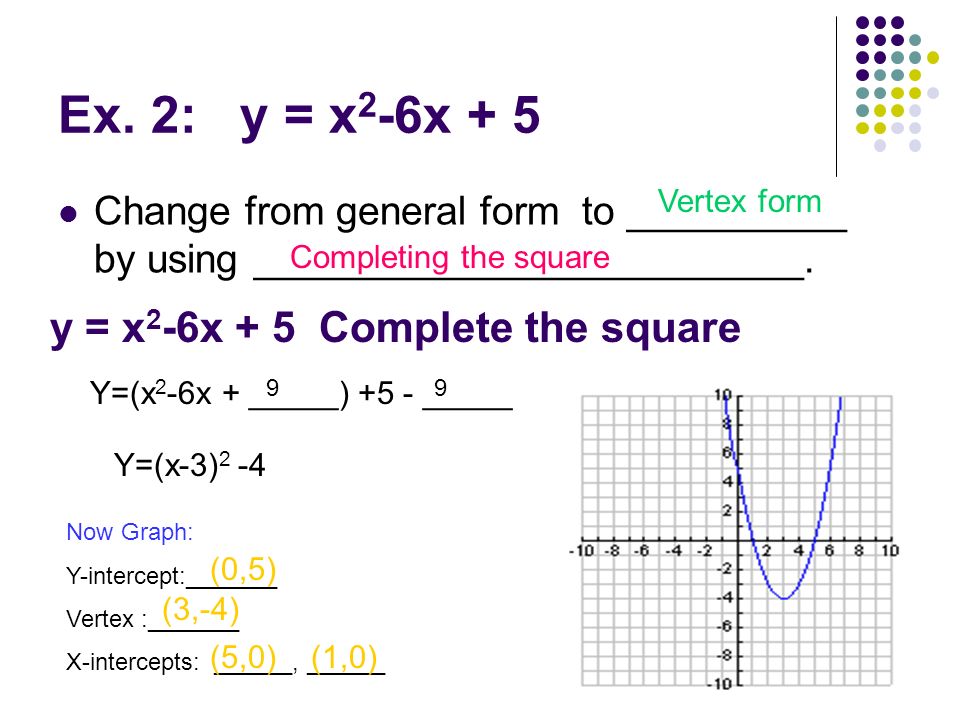
How do you convert functions standard form to vertex form?View Notes SolvingMethods 16docx from EE 6 at Texas State University Unit 4 Part 3 Methods of Solving Quadratic Equations Day 6 Factoring Review Day 7Find the Vertex Form y=x^22x8 y = x2 − 2x − 8 y = x 2 2 x 8 Complete the square for x2 −2x−8 x 2 2 x 8 Tap for more steps Use the form a x 2 b x c a x 2 b x c, to find the values of a a, b b, and c c a = 1, b = − 2, c = − 8 a = 1, b = 2, c = 8 Consider the vertex form of a parabola a ( x d) 2 e a



Untitled Document



Solution What Is The Vertex Form Of F X X 2 2x 5
Y = x 2 6x 5 2 y = x 2 – 2x – 8 3 y = 2x 2 – 8x 6 4 y = 3x 2 24x – 45 pplications of Quadratic Function ding minimum and maximum valu vertex is a maximum vertex is a minimum hting fixture manufacturer has daily productio ) = 25n 2 – 10n 800, where C is the daily co umber of light fixtures producedFree functions vertex calculator find function's vertex stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie PolicyComplete the square y = 2x^2 3x 7 = 2 (x^2 3/2 x) 7 = 2 (x^2 3/2 x 9/16) 7 2 (9/16) = 2 (x 3/4)^2 7 9/8 = 2 (x 3/4)^2 56/8 9/8 = 2




Vertex Form Vertex Form Vertex Form Is Another



What Would An Equation For A Quadratic Function In Vertex Form With Vertex 1 6 That Passes Through The Point 3 4 Be Quora
Vertex Form Of A Quadratic The vertex form of a quadratic is given by y = a(x – h) 2 k, where (h, k) is the vertexThe "a" in the vertex form is the same "a" as in y = ax 2 bx c (that is, both a's have exactly the same value) The sign on "a" tells you whether the quadratic opens up or opens downThink of it this way A positive "a" draws a smiley, and a negativeSo the xcoordinate of the vertex is Lets plug this into the equation to find the ycoordinate of the vertex Lets evaluate Start with the given polynomial Plug in Raise 1 to the second power to get 1 Multiply 2 by 1 to get 2 Negate any negatives Now combine like terms So the vertex is (1,9)We can convert to vertex form by completing the square on the right hand side;
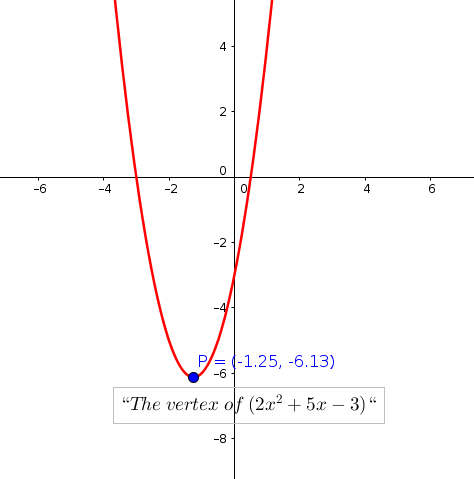



What Is The Vertex Form Of Y 2x 2 5x 3 Socratic



Put Y X 2 8x 3 In Vertex Form Youtube
Find the Vertex y=x^22x8 Rewrite the equation in vertex form Tap for more steps Complete the square for Tap for more steps Use the form , to find the values of , , and Consider the vertex form of a parabola Substitute the values of and into the formula Simplify the right sideOur perfect square trinomial factors into two identical binomials, (x6)•(x6) The vertex of an equation in vertex formBy comparing this with the vertex form of parabola, we get (h, k) ==> (3/2, 9/4) Example 5 y = x 2 2x 8 Solution By factoring negative from the quadratic function, we get y = (x 2 2x 8) y = (x 2 2x 8) y = (x 2 2 ⋅ x ⋅1 1 218) y = ((x1) 29) y = (x1) 2 9




Graph The Quadratic Function Y X 2 2x 3 Vertex X Y Intercepts Symmetry Domain Range Youtube




Answered C Complete The Table Sketch Each Bartleby
2 Input the xvalue of the vertex back into the quadratic to find the yvalue of the vertex 3 Input the vertex into the h and k values of the vertex form, which is y = a(x h)2 k 4 The a value is the coefficient in front of the x2 Convert to vertex form by completing the squareWrite the equation in vertex form {eq}y=x^22x8 {/eq} Vertex Form of a Parabola The vertex of a parabola is a point where the parabola has a maximum or a minimum value Complete the square to rewrite the quadratic function in vertex form y = x ^ 2 2x 8 Answers 3 Get Other questions on the subject Mathematics Mathematics, 1530, southerntouch103 Gretchen is setting up for a banquet she has 300 chairs and needs to distribute them evenly among t tables how many chairs should she put at




Vertex Intercept And Standard Form Ck 12 Foundation



Forms Of Quadratics Explanations Tips And Examples Albert Resources
We want to put it into vertex form y=a(xh) 2 k;Subtract y from both sides x^ {2}2xy8=0 All equations of the form ax^ {2}bxc=0 can be solved using the quadratic formula \frac {b±\sqrt {b^ {2}4ac}} {2a} The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction x=\frac {2±\sqrt {2^ {2}4\left (y8\right)}} {2}Statistics Arithmetic Mean Geometric Mean Quadratic Mean Median Mode Order Minimum Maximum Probability MidRange Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution Physics



What Is Vertex Form Example Get Education



Warm Up Find The Vertex The Roots Or The Y Intercept Of The Following Forms 1 F X X 4 F X 2 X 3 X 4 3 F X X 2 2x 15 Answers Ppt Download
10) Use your calculator to find the vertex, xintercepts, and yintercept Do they match yours?Parabola, Finding the Vertex 31 Find the Vertex of y = x 22x8 Parabolas have a highest or a lowest point called the Vertex Our parabola opens up and accordingly has a lowest point (AKA absolute minimum) We know this even before plotting "y" because the coefficient of the first term, 1 , is positive (greater than zero)Vertex Form Equation & Functions Just as y = mx b is a useful format for graphing linear functions, y = a(x h)^2 k is a useful format for graphing quadratic functions




Quadratic Equations And Quadratic Functions On The Sat



Vertex Form Of Quadratic Equation Mathbitsnotebook Ccss Math
Write the equation of the parabola in vertex form C y=3(x8)^2 2 Any number in the form of abi, where a and b are real numbers and b doesn't equal 0 is considered a pure imaginary number




Converting A Quadratic Function From Standard Form To Vertex Form Completing The Square Youtube



What Is The Axis Of Symmetry And Vertex For The Graph F X X 2 2x 8 Socratic



Www D105 Net Cms Lib Il Centricity Domain 610 Vertex practice worksheet answers Pdf



Ch 7 8




Write The Equation In Vertex Form Y X 2 2x 8 Study Com



Vertex Form Of A Quadratic Equation




The Vertex Form Of The Function Is Choose The Equation That Shows A Step In The Process Of Brainly Com




Graphing Parabolas



2




Vertex Form In 5 Minutes What Is Vertex Form How Do I Find It Mike S Calculators With Steps Free 21




Bingo Graphing Quadratics Parabolas In Vertex Form By Algebra Made Fun



3



Www Scasd Org Cms Lib Pa Centricity Domain 1229 2 2 a2 17 unit 2 2 ws packet lg Pdf




Vertex Form Of Quadratic Functions Math 2 Y



Draw The Graph Of The Polynomial F X X 2 2x 8 Sarthaks Econnect Largest Online Education Community




Transformations Of Quadratic Functions College Algebra



Why Is It In Vertex Form Of Quadratic Function Y A X H 2 K Getting Value Of H Is Opposite To Its Value Quora




6 3 Interpreting Vertex Form And Standard Form




Quadratic Functions




How To Go From Standard Form To Vertex Form By Completing The Square




2 C U K2f0w1c2k Akduote




How To Graph A Quadratic Equation 10 Steps With Pictures
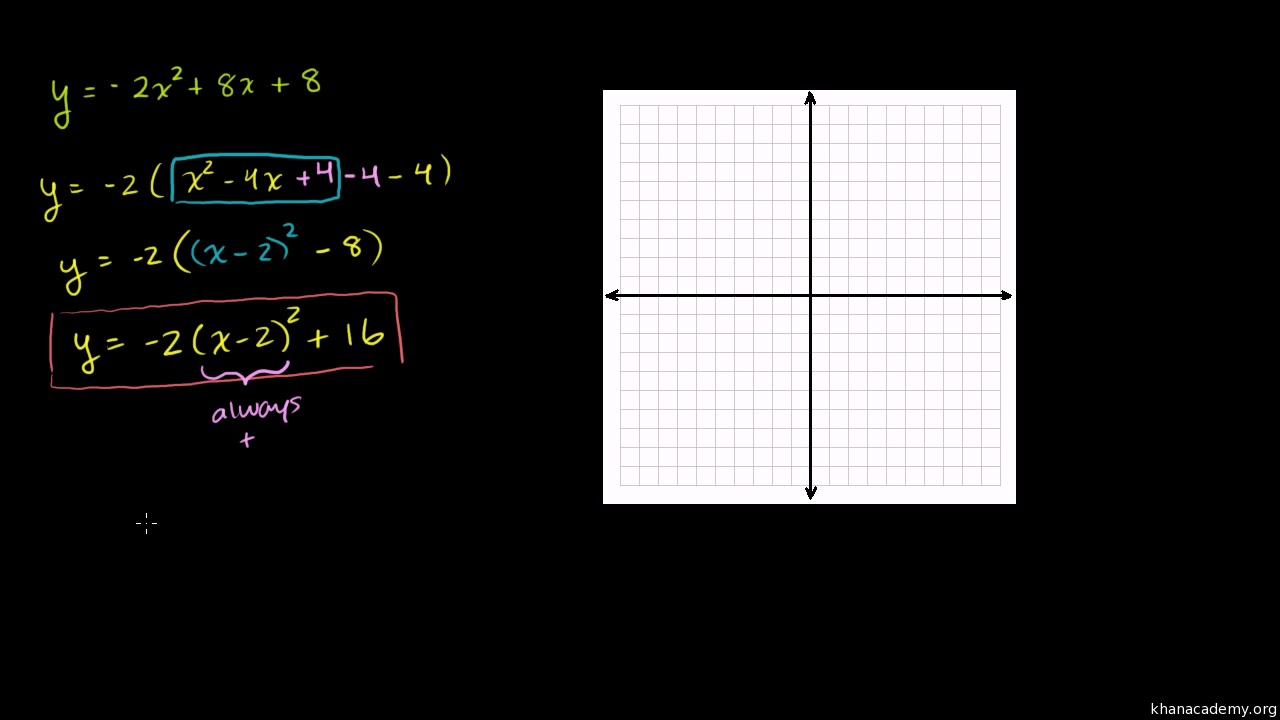



Vertex Axis Of Symmetry Of A Parabola Video Khan Academy




Draw The Graph Of The Polynomial F X X 2 2x 8




To Find The Vertex Transform The Quadratic Function From Standard Form To Vertex Form By Completing The Square Y 2x2 12x 10 2x2 6x 10 2x2 6x 9 18 10 2328 Square Meme On Awwmemes Com



Solution Write Each Function In Vertex Form Sketch The Graph Of The Function And Label Its Vertex 33 Y X2 4x 7 34 Y X2 4x 1 35 Y 3x2 18x 36 Y 1 2x2 5x



2 2 Characteristics Of Quadratic Functions Flip Ebook Pages 1 10 Anyflip Anyflip
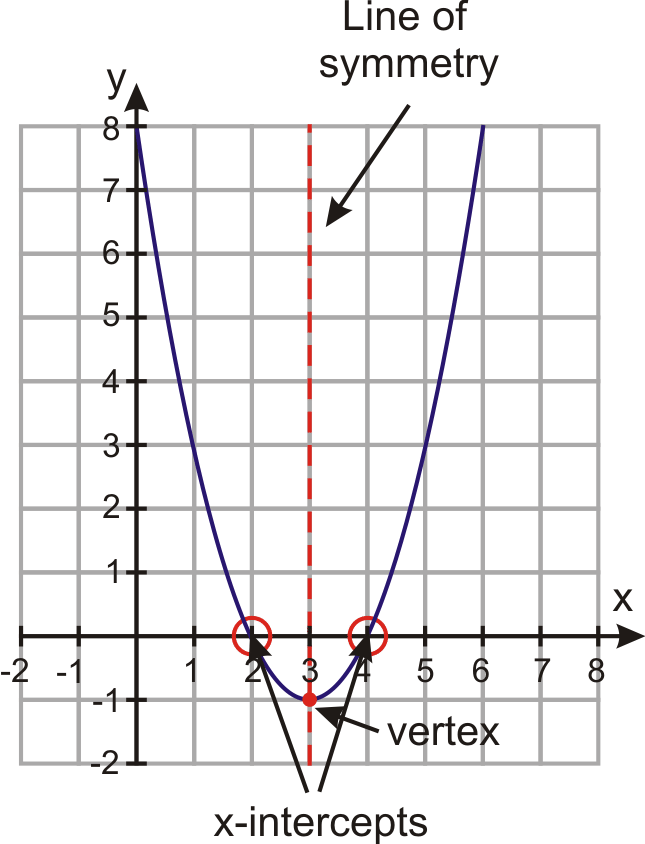



Graphs Of Quadratic Functions In Intercept Form Read Algebra Ck 12 Foundation



Biomath Quadratic Functions
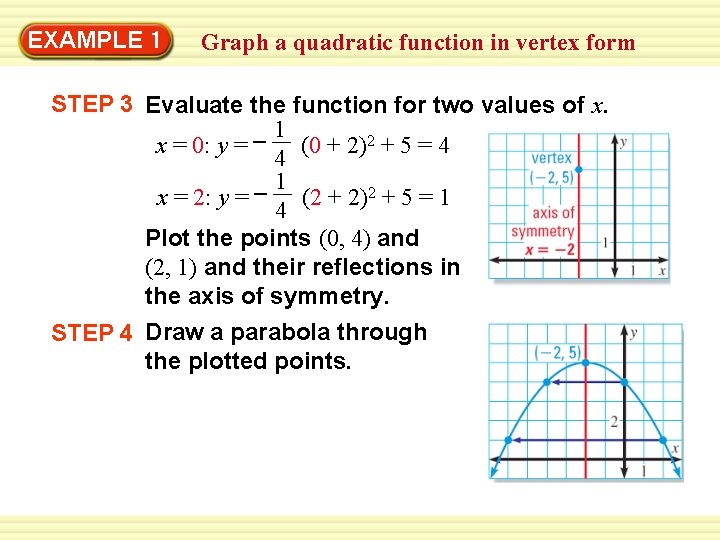



Vertex Form Of Quadratic Functions Math 2 Y
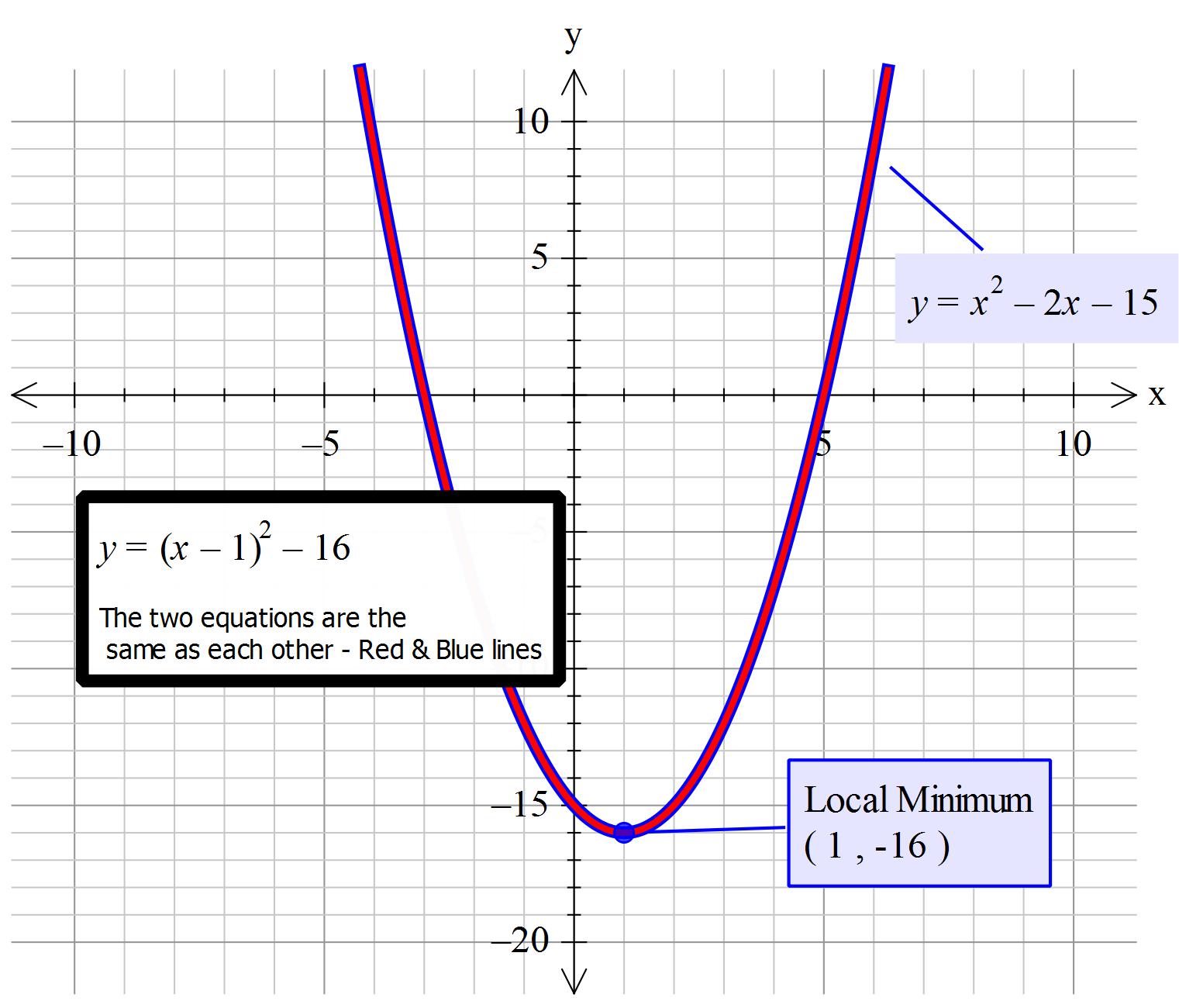



What Is The Vertex Form Of Y X 2 2x 15 Socratic




7 1 Graphs Of Quadratic Functions In Vertex Form Pdf Free Download




How To Go From Standard Form To Vertex Form By Completing The Square




Y X




How To Graph A Quadratic Equation 10 Steps With Pictures



How To Put An Equation Into Vertex Form Quora



Www Cbsd Org Cms Lib Pa Centricity Domain 3132 Day 1 graphing functions classwork and homework solutions Pdf




Fireworks From Standard To Vertex Form Ppt Video Online Download




Chris Is Asked To Graph The Quadratic Function F X Chegg Com




Sample Exam Grade 7




Mfg Problem Solving



Quadratic Functions



3 1 Graphs Of Quadratic Functions Mathematics Libretexts



Solution Use The Graph Of Y X 2 2x 8 Does This Function Have A Maximum And Minimum And If So What Are They




5 Write The Equation Of The Parabola In Vertex Form Chegg Com




7 1 Graphs Of Quadratic Functions In Vertex Form Quadratic Flip Ebook Pages 1 39 Anyflip Anyflip
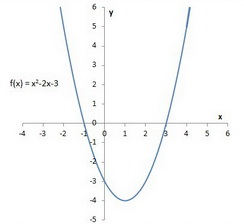



How Do I Convert The Equation F X X 2 2x 3 To Vertex Form Socratic




Mfg The Vertex Of A Parabola




8 The Relation Y X 12 4 Is Written In Vertex Fo Gauthmath




Vertex Form In 5 Minutes What Is Vertex Form How Do I Find It Mike S Calculators With Steps Free 21
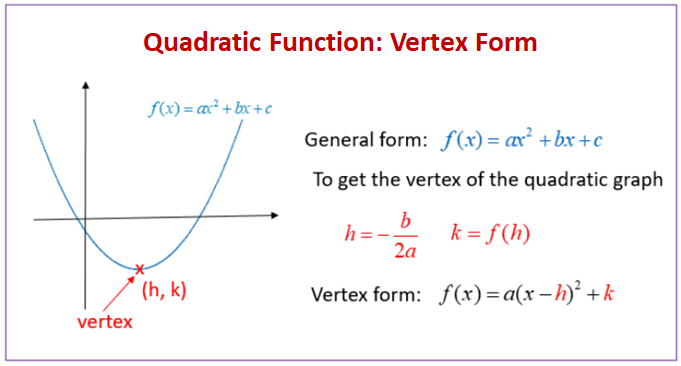



Quadratic Functions Examples Solutions Videos




Finding Features Of Quadratic Functions Video Khan Academy




7 1 Graphs Of Quadratic Functions In Vertex Form Quadratic Flip Ebook Pages 1 39 Anyflip Anyflip



Q Tbn And9gctwl8ksal48ks9fvcggchq7ifw Mt5nzxx1 0ivsjobxia io Usqp Cau




Vertex Form Of Parabolas Kuta Software Form Of Vertex Form Of Parabolas Date Period Use Pdf Document



Graphing Quadratic Functions
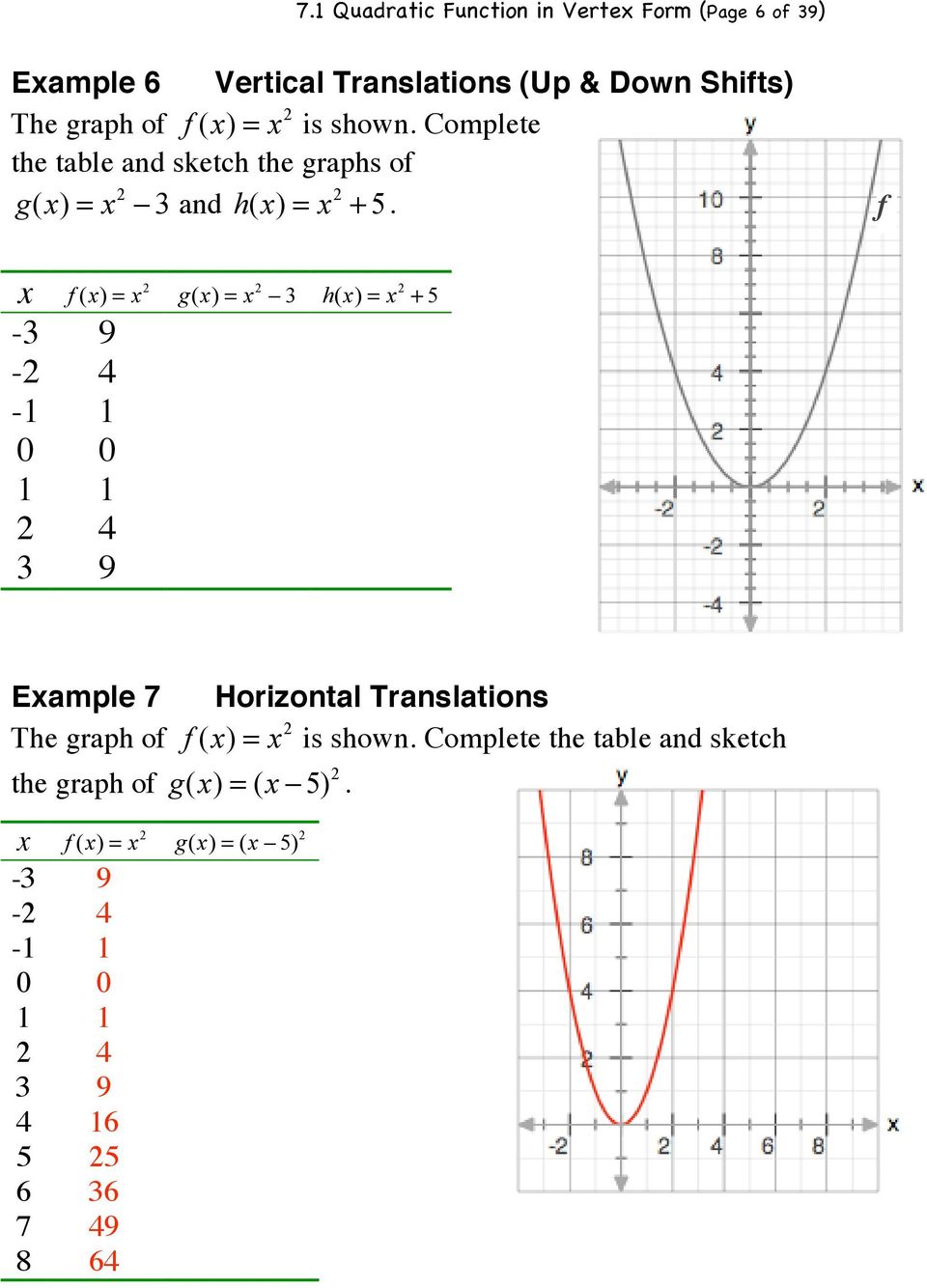



7 1 Graphs Of Quadratic Functions In Vertex Form Pdf Free Download



Http Www Mrsfruge Com Uploads 1 2 0 0 P2a 3 3 Quadratic Functions Packet Pdf
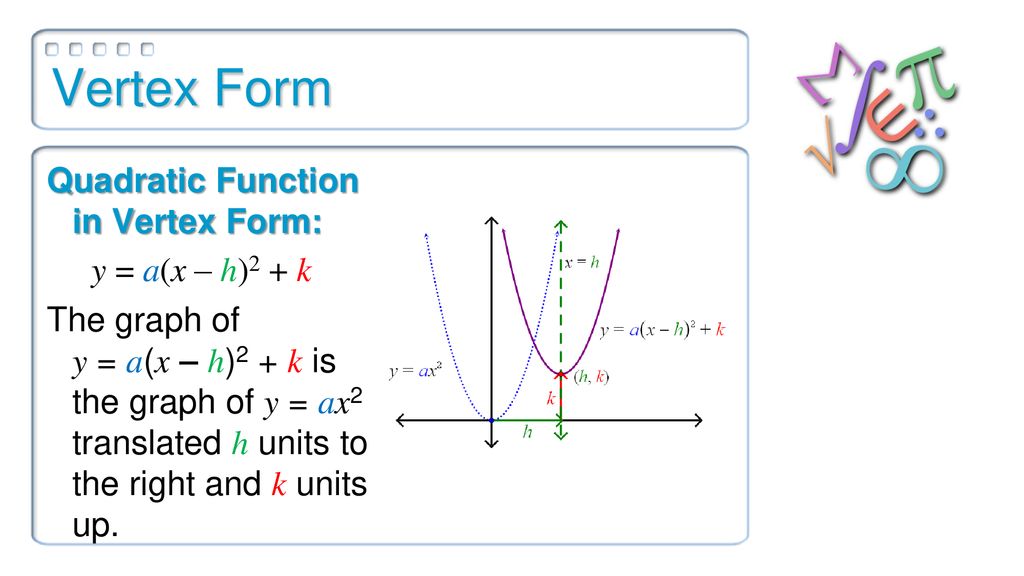



Vertex Form Quadratic Function In Vertex Form Ppt Download



1




The Vertex Form Of The Equation Of A Parabola Is Y 1 2 X 4 Squared 13 What Is The Standard Form Of Brainly Com




Given The Quadratic Yx22x 35 See How To Solve It At Qanda




Vertex Axis Of Symmetry Of A Parabola Video Khan Academy



Completing The Square Vertex Form Of A Quadratic Expii




Converting Quadratic Equations Ppt Download




Changing Quadratic Functions From Standard Form To Vertex Form Flashcards Quizlet




X2 2x 2 0 Quadratic Formula Novocom Top




Write X 2 4x 3 In The Form Y X H 2 K Chegg Com




Example 4 Write A Quadratic Function In Vertex Form Write In Vertex Form Then Identify The Vertex X 2x 2 10x 22 Y Solution X 2x 2 10x 22 Y Write Ppt Download
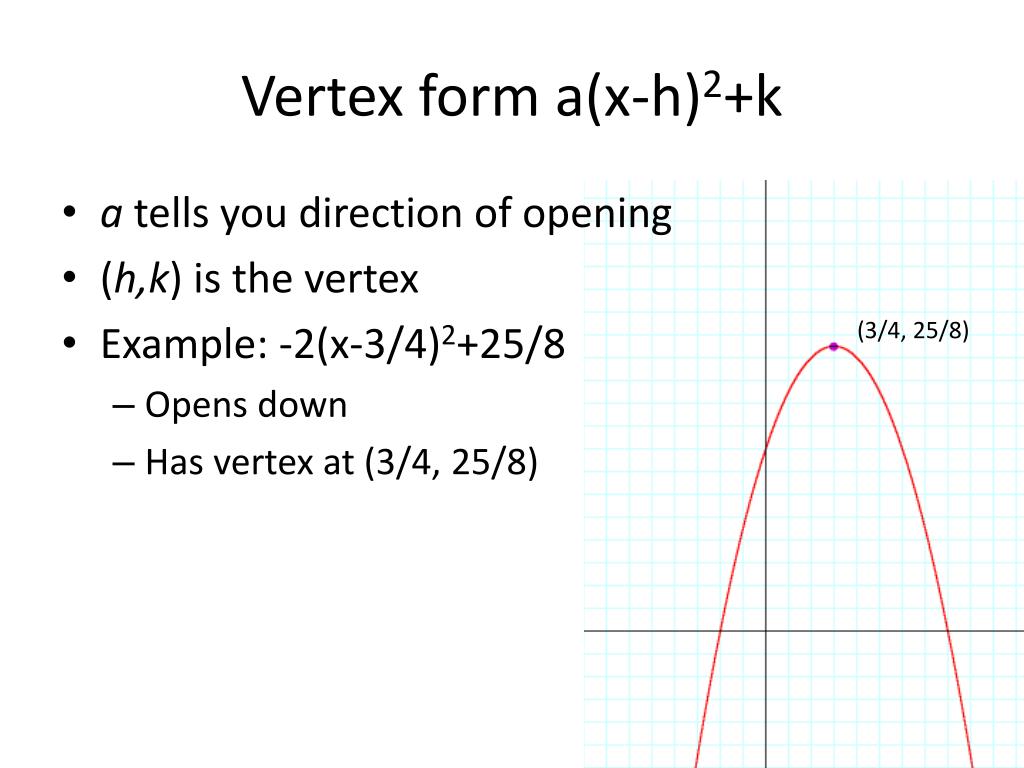



Ppt Vertex Form Powerpoint Presentation Free Download Id



Http Www Midwayisd Org Cms Lib Tx Centricity Domain 164 Preap alg ii 4 7b Pdf



Graphing Quadratic Functions



View Question What Is The Vertex Of The Equation Y X 2 2x 8



Http Www Tatecountyschools Org Userfiles 157 Classes 850 A3 review for test 3a Pdf Id




Vertex Form In 5 Minutes What Is Vertex Form How Do I Find It Mike S Calculators With Steps Free 21



Unit 8 Homework 3 Vertex Form Of A Quadratic Equation


