EduRev JEE Question is disucussed on EduRev Study Group by 185 JEE StudentsCancel (x 1) length = 2x 3 units The synthetic division method is in the attached pictureThe area of the region between the curves is defined as the integral of the upper curve minus the integral of the lower curve over each region The regions are determined by the intersection points of the curves This can be done algebraically or graphically Integrate to find the area between and
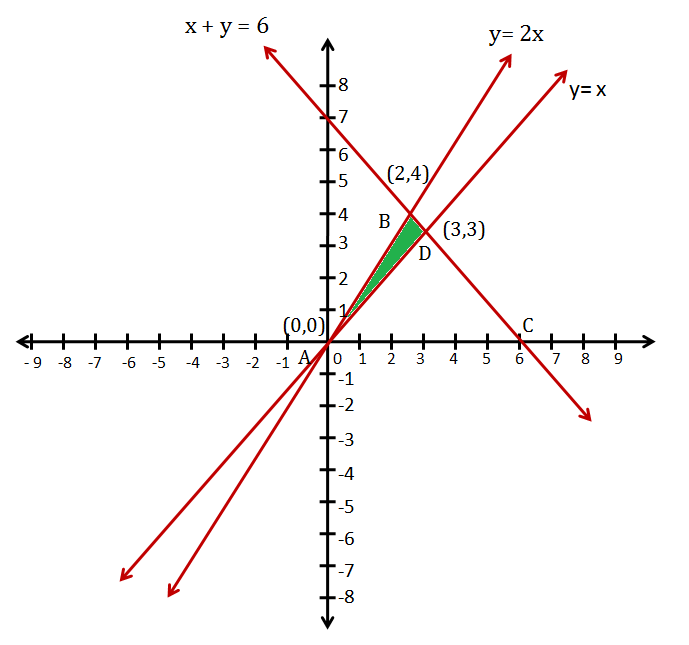
Determine Graphically The Co Ordinates Of The Vertices Of The Triangle Formed By The Equation Whose Sides Are Y X Y 2x X Y 6 Also Area And Co Ordinate Mathematics Topperlearning Com Ee7ugaa
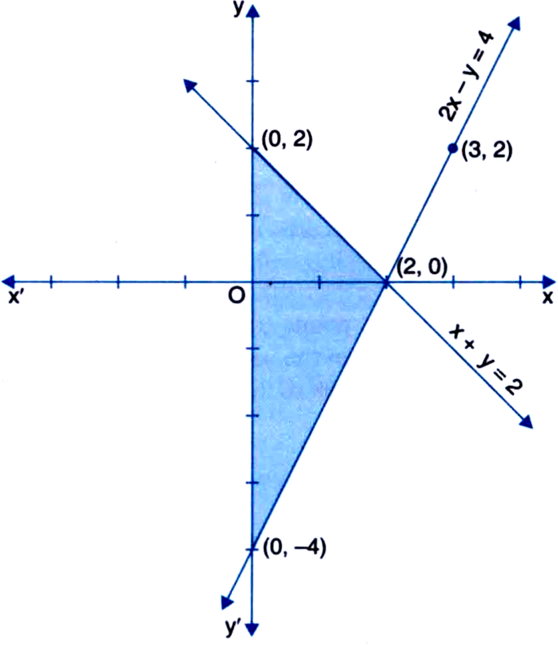
2x y=2 2y-x=4. what is the area of the triangle formed by these lines and the x-axis
2x y=2 2y-x=4. what is the area of the triangle formed by these lines and the x-axis-In graph we find that the lines are intersecting at (1, 4) Hence x = 1, y = 4 is the solution of the equationsThe two triangles are ABC and DBE Area of ABE = × Base × perpendicular Area of ADC = × Base × perpendicular ABE area ADC Area The triangular region bounded by the lines y=2x1, y=3x1 and x=4 is represented graphically as Equations of the lines are y=2x1,y=3x1 and x4 Let y 1 =2x 1, y 2 = 3x1 Now area of the triangle bounded by the given lines = 8 square units Thus, the area of the required triangular region is 8 sq units



Solve Graphically The System Of Equations 2x 3y 12 X 3y 6 Find The Coordinates Of The Vertices Of The Triangle Formed By These Two Lines And The Y Axis Mathematics Shaalaa Com
A line that runs parallel to the \(x\)axis is called a horizontal line and has a gradient of zero This is because there is no vertical change \m = \frac{\text{change in } y}{\text{change in } x} = \frac{0}{\text{change in } x} = 0\ A line that runs parallel to the \(y\)axis is called a vertical line and its gradient is undefined What is the area of triangle formed by line 2x3y=12 with the coordinate axes?Solution Question 39 Draw the graphs of the following equations x y — 5;
The zeros are 4 and 12 Function 2 and 3 intersect in P (0,4) 61E Exercises for Section 61 For exercises 1 2, determine the area of the region between the two curves in the given figure by integrating over the xaxis For exercises 3 4, split the region between the two curves into two smaller regions, then determine the area by integrating over the xOf the tetrahedron The base is the triangle in the xyplane sketched below What's the equation for the line?
In Geometry, a triangle is a threesided polygon that has three edges and three vertices The area of the triangle is the space covered by the triangle in a twodimensional plane The formula for the area of a triangle is (1/2) × base × altitude Let's find out the area of a triangleThe area of the triangle formed by the lines 3x 2y = 8, 2x y = 1 and the xaxis has to be determined First, determine the point of intersection of the lines 3x 2y = 8 and 2x y = 1Solve the Following System of Equations Graphically 2x = 23 3y 5x = 8y Also, Find the Area of the Triangle Formed by These Lines and Xaxis in Each Graph



Class 10 Maths Graphical Questions For Linear Equations In Two Variables



Draw Graphs For Following Equations On The Same Graph Paper 2x Y 2 2x Y 6 Find Co Ordinates Of The Vertices Of Trapezium Formed By These Lines Also
Question A triangle is formed by the intersection of the lines 2x 3y = 14 4X 5y= 16 and the x axisFind the area of the triangle Thank you so much Answer by ReadingBoosters(3246) (Show Source) Clearly, we can scale the coefficients of a given linear equation by any (nonzero) constant and the result is unchanged Therefore, by dividingthrough by $\sqrt{a_i^2b_i^2}$, we may assume our equations are in "normal form"The area of the triangle formed the lines x=3, y=4 and x=y is MCQ Chapter 3 RD Class 10 🔥🔥 The area of the triangle formed the lines x=3, y=4 and x=y is MCQ Chapter 3




Solve The Following Pair Of Equations Graphically X 3y 6 2x 3y 12 Also Find The Area Of The Brainly In




Solution Find The Angle Formed By The Lines 2x Y 8 0 And X
math 1)The area A of a triangle varies jointly as the lengths of its base b and height h If A is 75 when b=15 and h=10,find A when b=8 and h=6 2)Determine the equation of any vertical asymtotes of the graph of f (x)=2x3/x^22x3 1)X − 2 = 0 x 2 = 0 Add 2 2 to both sides of the equation x = 2 x = 2 x = 2 x = 2 The final solution is all the values that make x ( x − 2) = 0 x ( x 2) = 0 true x = 0, 2 x = 0, 2 x = 0, 2 x = 0, 2 x = 0, 2 x = 0, 2 Substitute 0 0 for x x into y = 2 x y = 2 x then solve for y y Given 2xy=2 , 2yx=4 To Find the area of a triangle formed by the two lines and the line y=0 Solution 2xy=2 2yx=4 y = 0 2xy=2 , y = 0 => point of intersection ( 1 , 0) 2yx=4 , y = 0 => point of intersection ( 4 , 0) 2xy=2 , 2yx=4 => point of intersection ( 0 , 2) Triangle is formed with base = ( 1 (4) = 5 Height = 2



R D Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2




Determine Graphically The Co Ordinates Of The Vertices Of The Triangle Formed By The Equation Whose Sides Are Y X Y 2x X Y 6 Also Area And Co Ordinate Mathematics Topperlearning Com Ee7ugaa
🔴 Answer 3 🔴 on a question The area of a triangle is 1/2 (x^2 2x 2x^2 4) the height h is x2 write an expression for the base b of the triangle ( hint area of a triangle 1/2 bh) the answers to ihomeworkhelperscom Given 2xy=2 , 2yx=4 To Find the area of a triangle formed by the two lines and the line y=0 Solution 2xy=2 2yx=4 y = 0 2xy=2 , y = 0 => point of intersection ( 1 , 0) 2yx=4 , y = 0 => point of intersection ( 4 , 0) 2xy=2 , 2yx=4 => point of intersection ( 0 , 2) Triangle is formed with base = ( 1 (4) = 5 Height = 2 asked in Class X Maths by saurav24 Expert (14k points) Draw the graph of the pair of equations 2x y= 4 and 2x – y = 4 Write the vertices of the triangle formed by these lines and the yaxis, find the area of this triangle?



What Is The Area Of The Triangle Formed By 2x 3y 6 And The Coordinate Axes Quora




Solve The Equations Graphically 2x Y 2 2y X 4 Also Find The Area Of A Triangle Fo Brainly In
Xy = 5 (i) Find the solution of the equations from the graph (ii) Shade the triangular region formed by the lines and theyaxis Solution 10Answer 2xy = 4(i) ⇒ y = 4−2x If x= 0,y = 4−2(0)= 4−0 =4 x = 1,y = 4−2(1) = 4−2= 2 x = 2,y = 4−2(2) = 4−4= 0 x 0 1 2 3 y 4 2 0 −2 (i) A B C −2If 2x^23xyy^2=0 represents two sides of a triangle and lxmyn=0 in the third side then locus of incentre of the triangle is
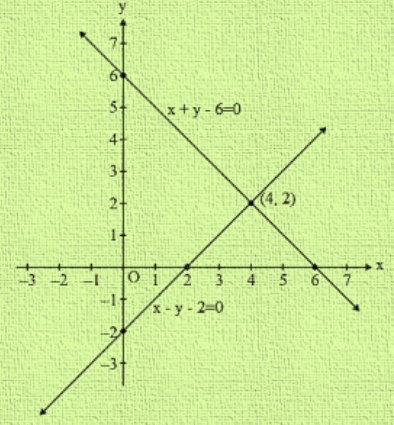



R D Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2




Misc 8 Find Area Of Triangle Formed By Y X 0 X Y 0
2x y = 2;' pair of linear equations in two variables Solve graphically 2x y = 2 and 4x y = 4, shade the region between these lines and the yaxis Asked by Topperlearning User 31st Aug, 17, 0335 PM Expert Answer
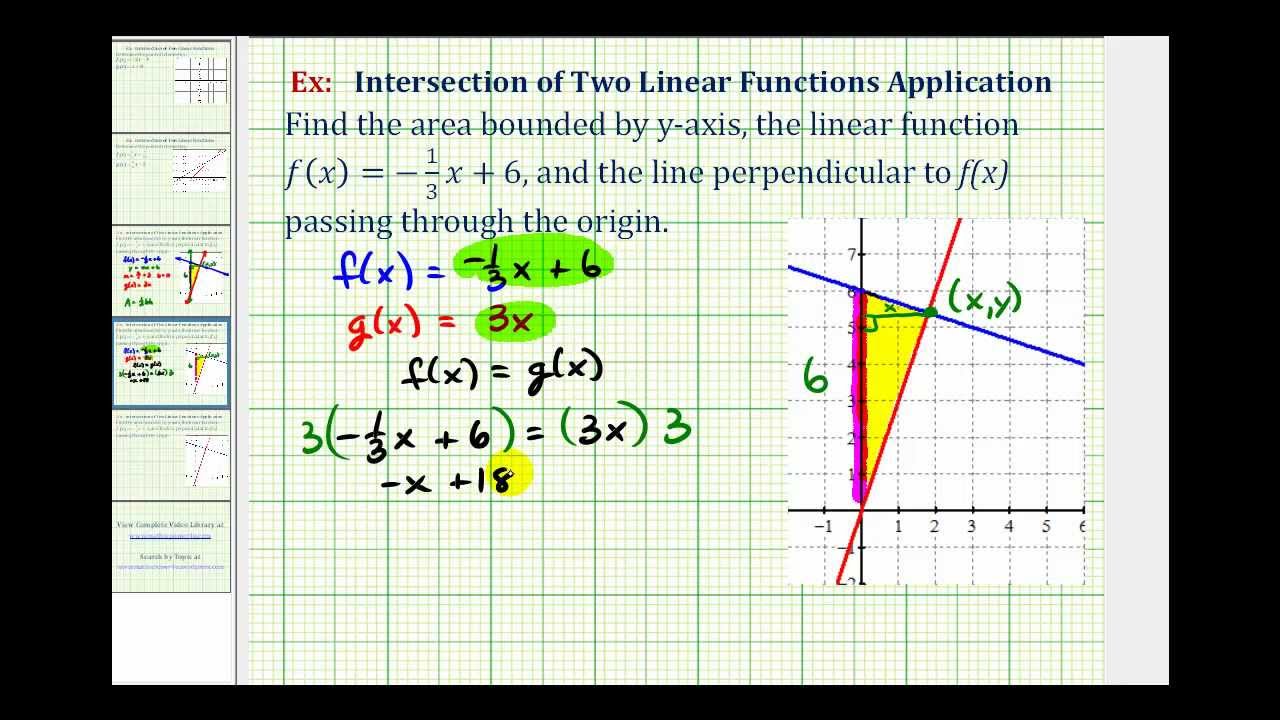



Ex Find The Area Of A Triangle Bounded By A Line A Perpendicular Line And The Y Axis Youtube




Draw The Graph Of 2x Y 6 And 2x Y 2 0 Shade The Region Bounded By These Lines And X Y Find The Area Of The Shaded Region
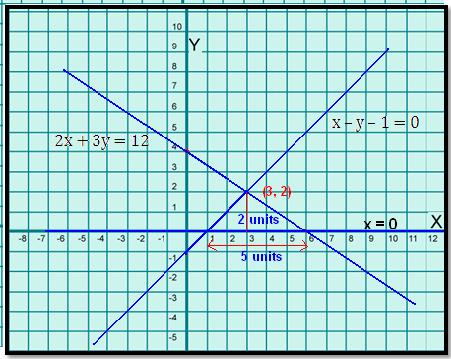
Well, this is the line with z= 0, so 2x 4y= 8, which amounts to y= 2 x 2 From the picture, we can see that xgoes from 0 to 4 For a given value of x, ygoes from 0 to 2 xHere, the line 2xy=2 cuts the xaxis at (–4,0) and line 2y–x=4 cuts the xaxis at (1,0) and point of intersection of these lines is (0,2) So, the points (–4,0), (0,2) & (1, 0) formed a triangle in which point point (0, 2) lie on yaxis , ie 2 units hight from origin and points (4,0) & (1, 0) lie on xaxis in which distance between these 1(4) =14 = 5 units To calculate the Area at first we solve the Equation 1 & 2 Simultaneously by method of substitution We substitute the value of x from Equation 2 in Equation 1 to get the value of y Equation 2 x – y = 1 ⇒ x = y 1 Equation 1 2x 3y = 12 Substituting the value from equation 2 we get 2(y 1) 3y = 12 ⇒ 2y 2 3y = 12 ⇒ 5y = 10 ⇒ y = 2



Draw The Graph Of The Pair Of Equations 2x Y 4 And 2x Y 4 Studyrankersonline




Solve Graphically The System Of Equations 2x 3y 12 X 3y 6 Find The Coordinates Of The Vertices Of The Triangle Formed By These Two Lines And The Y Axis Mathematics Shaalaa Com
2yx = 4 What is the area of the triangle formed by the two lines and the liney = 0?SolutionShow Solution y = 2 – 2x (i) Now, plot the points A (0, 2), B (1, 0) and C (2, 2) on a graph paper and join A, B and C to get the graph of 2x y = 2 y = 6 – 2x (ii) Now, plot the points D (0,6), E (1, 4) and F (3,0) on the same graph paper and join D, E and F to get the graph of 2xA triangle is formed by the xaxis and the lines 2x y = 4 and x y 1 = 0 as three sides Taking the side along xaxis as its base, the corresponding altitude of the triangle is 3 units



Shade The Triangle Formed By The Graphs Of 2x Y 4 X Y 2 And The Y Axis Write The Coordinates Of Vertices Of The Triangle From Mathematics Linear
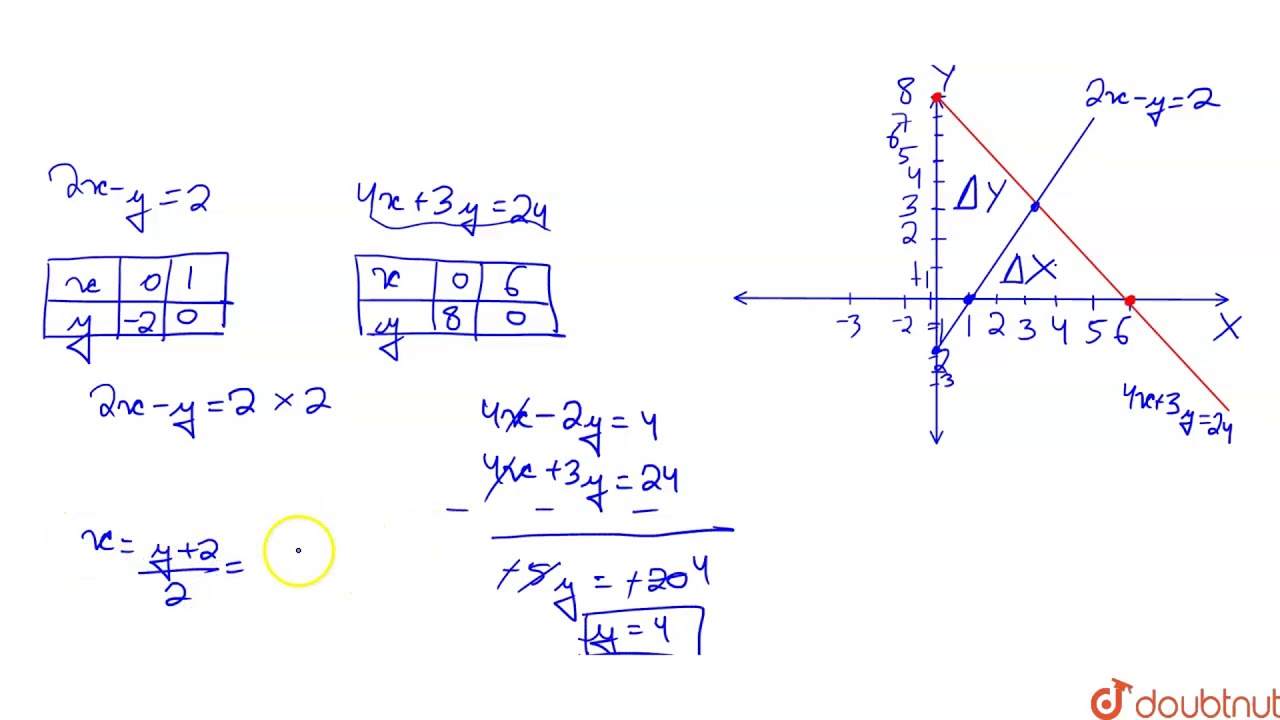



Draw The Graphs Representing The Equations 2x Y 2 And 4x 3y 24 On The Same G Youtube
Explanation Circle 1 x2 y2 6x = 0, ⇒ center C1 = ( −3,0),r1 = 3, Circle 2 x2 y2 −2x = 0, ⇒ center C2 = (1,0),r2 = 1 As the two circles touch each other externally, they have 3 common tangents Obviously, Yaxis (x = 0) is one of the common tangents Let y = mx c be the equation of the other tangents What is the area, in square units, of the triangle bounded by y=0, y=x4 and x3y=12 ?RD Sharma Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations In Two Variables Exercise 32 The knowledge of the construction of graphs of linear equations in solving systems of simultaneous linear equations in two variables is practised in this exercise The RD Sharma Solutions Class 10 can be a great help for students for




Draw The Graphs Of The Equations X 3 X 5 And 2x Y 4 0 Also Find The Area Of The Quadrilateral Youtube



Draw The Graph Of 2x Y 6 And 2x Y 2 0 Shade The Region Bounded By These Lines And X Axis Find The Area Of The Shaded Region Sarthaks Econnect Largest Online Education Community
The given pair of straight lines is 2 xy4 = 0 and x y 1 = 0 As, the area formed by the triangle formed by these lines with the xaxis is to be found Solving the equations of lines for y = 0, we get their points of intersection with the xaxis as B 2, 0 and C1, 0 respectively1Graphically, solve the following pair of equations 2x y = 6 and 2x y 2 Find the ratio of the areas of the two triangles formed by the lines representing these equations with the Xaxis and the lines with the Yaxis Ans 41 2Determine graphically, the vertices of the triangle formed by the lines y =3, x = 3y, and x y = 8 We join D,E and F and extend it on the both sides to obtain the graph of the equation 2x y 2 = 0 It is evident from the graph that the two lines intersect at point F (1,4) The area enclosed by the given lines and xaxis is shown in Fig above Thus, x = 1, y = 4 is the solution of the given system of equations




Ex 3 2 7 Draw Graphs Of X Y 1 0 And 3x 2y 12 0



Draw The Graph Of The Following Equation On The Same Graph Paper 2x Y 2 2x Y 6 What Is The Area Of A Trapezium Formed By These Lines Quora
Jun 14,21 The area of triangle formed by the lines y = x, y = 2x and y = 3x 4 isa)8b)7c)4d)9Correct answer is option 'C' Can you explain this answer? The volume of the solid generated by y = 2x, y = x^2 revolved about the xaxis is (64pi)/15 Revolving the area between these two curves about the xaxis, we end up with something that looks sort of like a cone a hollow cone, with a curved inside Now, imagine for a second taking a cross section parallel to the yz plane, cutting the cone down the middleFind the area of the region bounded by lines 2x y = 4, 3x – 2y = 6 Using the method of integration




Class 10 Mathematics Chapter 3 Ncert Exemplar Solution Part Iva
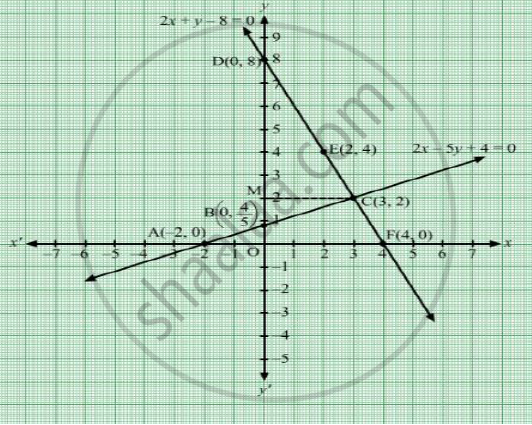



Solve Graphically The System Of Equations 2x 5y 4 0 2x Y 8 0 Find The Coordinates Of The Vertices Of The Triangle Formed By These Two Lines And The Y Axis Mathematics Shaalaa Com
2 4 5 Obtuse scalene triangle, area=38 Computed angles, perimeter, medians, heights, centroid, inradius and other properties of this triangle The area of a rectangle have the formula A = lw To find the length of the given triangle, divide the area by the width There are several ways to do this, so I'll be using synthetic division and cancellation;Factor out the trinomial;
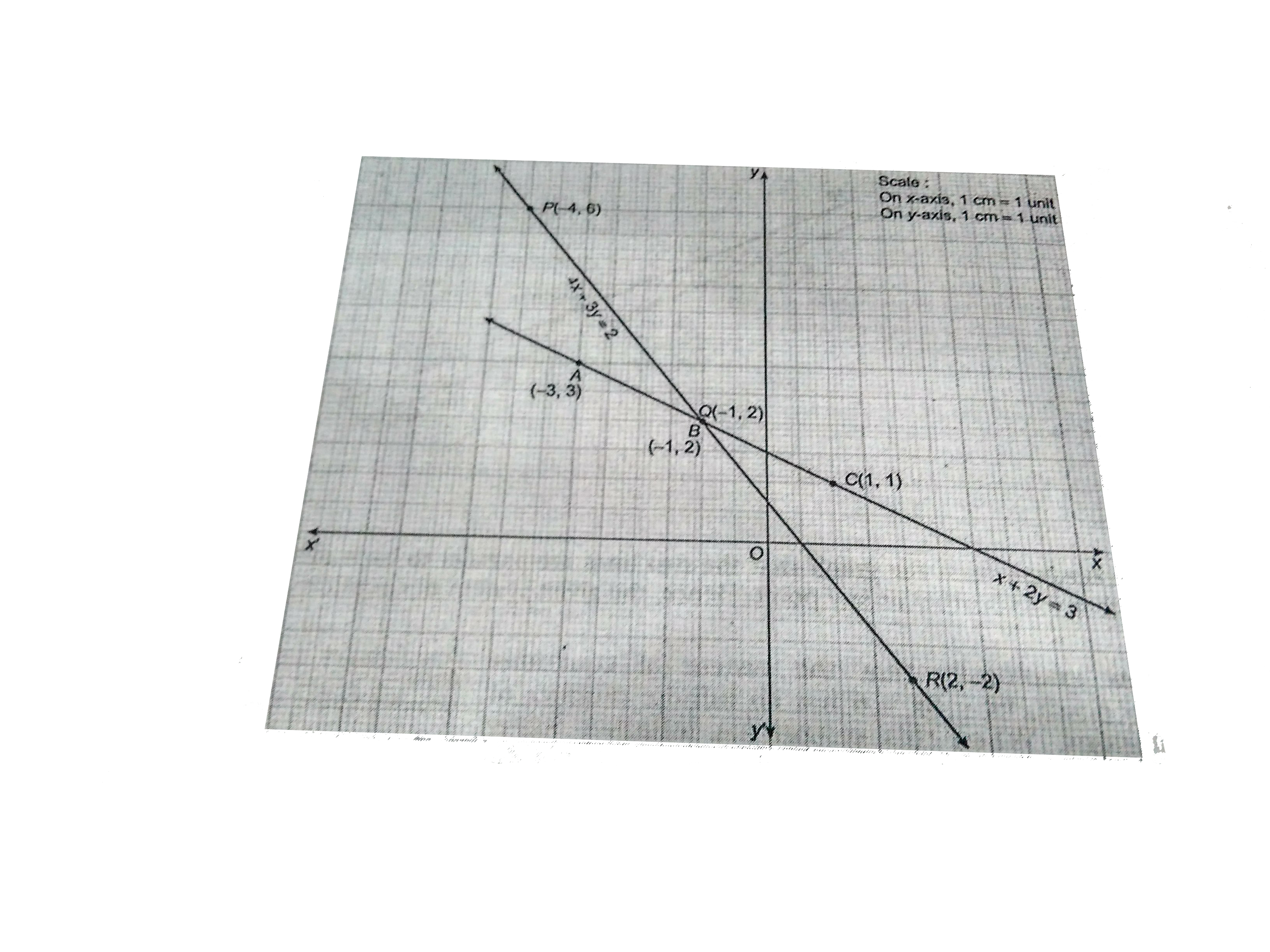



Show Graphically The System Of Linear Equations X 2y 3



What Is The Centroid Of The Triangle Formed By The Line 2x 3y 6 0 With Its Coordinate Axes Quora
0 2 We plot the points (2, 0) and (0, 2) on the same graph paper and join the same by a ruler to get the line which is the graph of the equation x y = 2 From graph, we see that the coordinates of the vertices of the triangle are (2, 0), (0, 2) and (0, –4) The triangle has been shadedHere, the line 2xy=2 cuts the xaxis at (–4,0) and line 2y–x=4 cuts the xaxis at (1,0) and point of intersection of these lines is (0,2) So, the points (–4,0), (0,2) & (1, 0) formed a triangle in which point point (0, 2) lie on yaxis , ie 2 units hight from origin and points (4,0) & (1, 0) lie on xaxis in which distance between these 1(4) =14 = 5 unitsWas asked on View the answer now




Solve The Equations Graphically 2x Y 2 2y X 4 Also Find The Area Of The Triangle Formed By Two Lines Brainly In
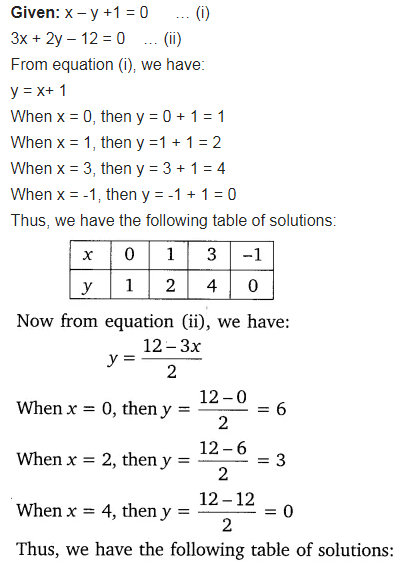



Draw The Graphs Of The Equations X Y 1 0 And 3x 2y 12 0 Cbse Class 10 Maths Learn Cbse Forum
Misc 14 Using the method of integration find the area of the region bounded by lines 2𝑥 𝑦 = 4, 3𝑥–2𝑦=6 and 𝑥–3𝑦5=0 Plotting the 3 lines on the graph 2𝑥 𝑦 = 4 3𝑥 – 2𝑦 = 6 𝑥 – 3𝑦 5 = 0 Find intersecting Points A & B Point A Point A is intersection of lines x – 3y 5Question Find the area of the triangle formed by the (x,y)axes and the line with equation 4x3y12=0 Answer by KMST(52) ( Show Source ) You can put this solution on YOUR website! Consider, 2x 3y = 12 Consider, x – y – 1 = 0 Let's plot the graph now From the figure, notice that the base of the triangle = 5 units Altitude = 2 units Hence area of triangle = (1/2) × 5 × 2 = 5 sq units Recommend (0) Comment (0) person Kishore Kumar




Draw The Graphs Of 2x Y 6a N D2x Y 2 0 Shade The Region Boun Ded By These Lines And X Ax Youtube
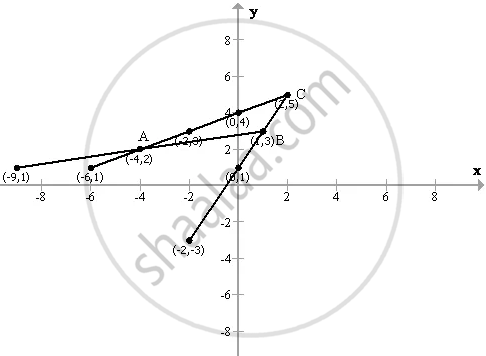



Find Graphically The Vertices Of The Triangle Whose Sides Have The Equations 2y X 8 5y X 14 And Y 2x 1 Respectively Take 1 Cm 1 Unit On Both The Axes Mathematics Shaalaa Com
If area of the triangle formed by (0, 0), (a^ (x^2), 0), (0, a^ (6x)) is 1/ (2a^5) sq units then x= This browser does not support the video element Step by step solution by experts to help you in doubt clearance & scoring excellent marks in exams The area of the triangle formed by the lines and isSo, AOQD is formed by these lines Hence, the vertices of the A00D formed by the given lines are0(0, 0),Q(4, 4)and 0(6,2) Question 3 Draw the graphs of the equations x = 3, x = 5 and 2x – y – 4 = 0 Also find the area of the quadrilateral formed by the lines and the Xaxis SolutionCorrect answer to the question Draw the graph representing the equations xy=1 and 2x 3y = 12 on the same graph paper , find the area of the triangles formed by theselines, the xaxis and the yaxis brainsanswersincom



Draw The Graphs Of The Pair Of Linear Equations X 2y 5 And 2x 3y 4 Also Find The Points Where The Lines Meet The X Axis Sarthaks Econnect Largest Online Education Community



Compute The Area Bonded By The Lines X 2y 2 Y X 1 And 2x Y 7 Studyrankersonline
Solution A line through (5, 2) and (1, 4) is perpendicular to the line through Solution The line 2x–3y2=0 is perpendicular to another line L1 of unknown equation Solution Determine B such that 3x2y–7=0 is perpendicular to 2x–By2=0The triangle form by the graph of 2xy=4 and xy=2 and y axis (i) Find the point of intersection of two lines(ii) Write the coordinates of vertices of the triangle(iii) Find the area of triangle(iv) Write the formula of area of triangle which you use for this problems




Draw The Graphs Of X Y 1 0 And 3x 2y 12 0 Determine The C




Draw The Graph Of The Pair Of Equations 2x Y 4 And 2x Y 4 Write The Vertices Of The Triangle Youtube




Find The Area Of Triangle Formed By The Lines X Y 6 0 X 3y 2




Find Graphically The Co Ordinates Of The Vertices Of The Triangle Formed By The Lines Y 0 Y X And 2x 3y 10 Hence Find The



How Will You Find The Coordinates Of Vertices Of A Triangle Graphically Formed By The Lines 2y X 8 5y X 14 Y 2x 1 Quora




Draw The Graphs Of X Y 1 0 And 3x 2y 12 0 Determine The Coordinates Of The Vertices Of The Triangle Formed By These Lines And X Axis And Shade The Triangular Area



Represent The System Of Equations 4x Y 4 And 4x Y 12 Graphically Determine The Vertices Of The Triangle Formed By These Lines And The X Axis Shade The Mathematics Topperlearning Com 0ex2c5mqq
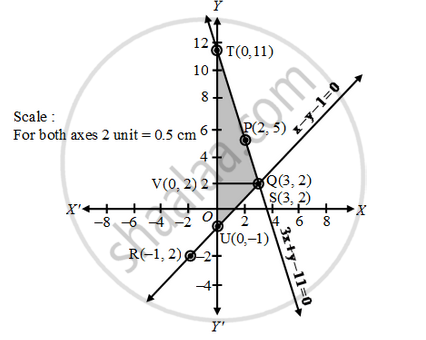



Solve The Following System Of Linear Equations Graphically 3x Y 11 0 X Y 1 0 Shade The Region Bounded By These Lines And Also Y A Mathematics Shaalaa Com



Draw The Graphs Of The Equations X Y 1 0 And 3x 2y 12 0 Determine The Coordinates Of The Vertices Of The Triangle Formed By These Lines And The X Axis Mathematics Topperlearning Com 7tnslr9gg




Draw The Graphs Of X Y 1 0 And 3x 2y 12 0 Determine The C




What Is The Area Of A Triangle Bounded By The Lines Y 0 X Y 0 And X 4 0 Quora
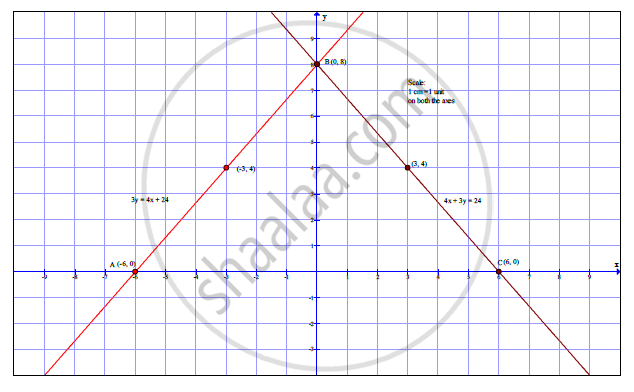



Draw The Graphs Representing The Equations 4x 3y 24 And 3y 4x 24 On The Same Graph Paper Write The Co Ordinates Of The Point Of Intersection Of These Lines And Find The



Draw The Graphs Of The Pair Of Linear Equations X 2y 5 And 2x 3y 4 Also Find The Points Where The Lines Meet The X Axis Sarthaks Econnect Largest Online Education Community




Use A Single Graph And Draw The Graph Of The Following Equations 2y X 8 5y X 14 Y 2x 1 Obtain The Brainly In



What Is The Area Of A Triangle Formed By The Lines X 0 Y 0 And 4x 5y Quora



Find Area Of The Triangle Formed By Lines Y X X 6 And Y 0 Linear Equations In Two Variables Maths Class 9




Question 7 Draw The Graphs Of The Equations X Y 1 0 And 3x 2y 12 0 Determine The Brainly In




Draw The Graphs Of 2x Y 6 And 2x Y 2 0 Shade The Region B




The Area Of The Triangle Formed By The Line X 3 Y 4 And



Draw The Graph Of Two Lines Whose Equations Are 3x 2y 6 0 And X 2y 6 0 On The Same Graph Paper Sarthaks Econnect Largest Online Education Community




Draw The Graph Of The Equations 2x Y 6 0 And 2x Y 6 0 Also Determine The Coordinates Of The Vertices Of The Triangle Formed By These Lines And The X Axis




Graphically Solve The Following Pair Of Equations 2x Y 6 And 2x Y 2 0 Find The Ratio Of The Areas Youtube
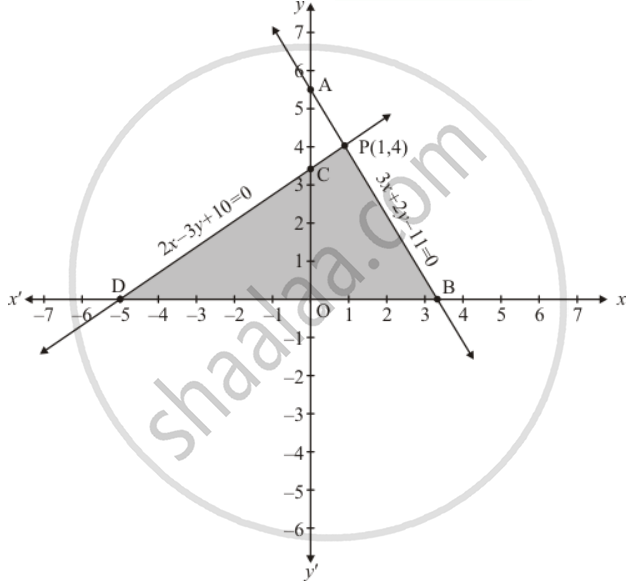



Solve The Following System Of Linear Equations Graphically And Shade The Region Between The Two Lines And X Axis 3x 2y 11 0 2x 3y 10 0 Mathematics Shaalaa Com



Solve The Following Pair Of Linear Equations Graphically 2x 3y 12 And X Y 1 Sarthaks Econnect Largest Online Education Community




Solve The Following System Of Equations Graphically 4x 5y 16 0 2x Y 6 Determine The Brainly In
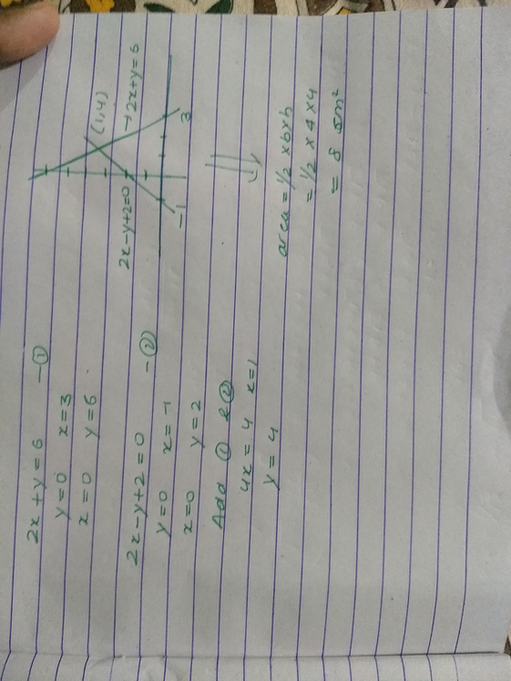



Draw The Graphs Of The Lines 2x Ty 6 And 2x Y 2 0 Shade The Scholr




Draw The Graphs Representing The Equation 2x Y 2 And 4x 3y 24 On The Same Graph Paper Find The Brainly In



How To Solve The Equations 2x Y 2 And 2y X 4 What Is The Area Of A Triangle Formed By The Two Lines And The Line Y 0 Mathematics Made Easy



Draw The Graphs Of The Lines Represented By The Equations X Y 4 And 2x Y 2 In The Same Graph Sarthaks Econnect Largest Online Education Community
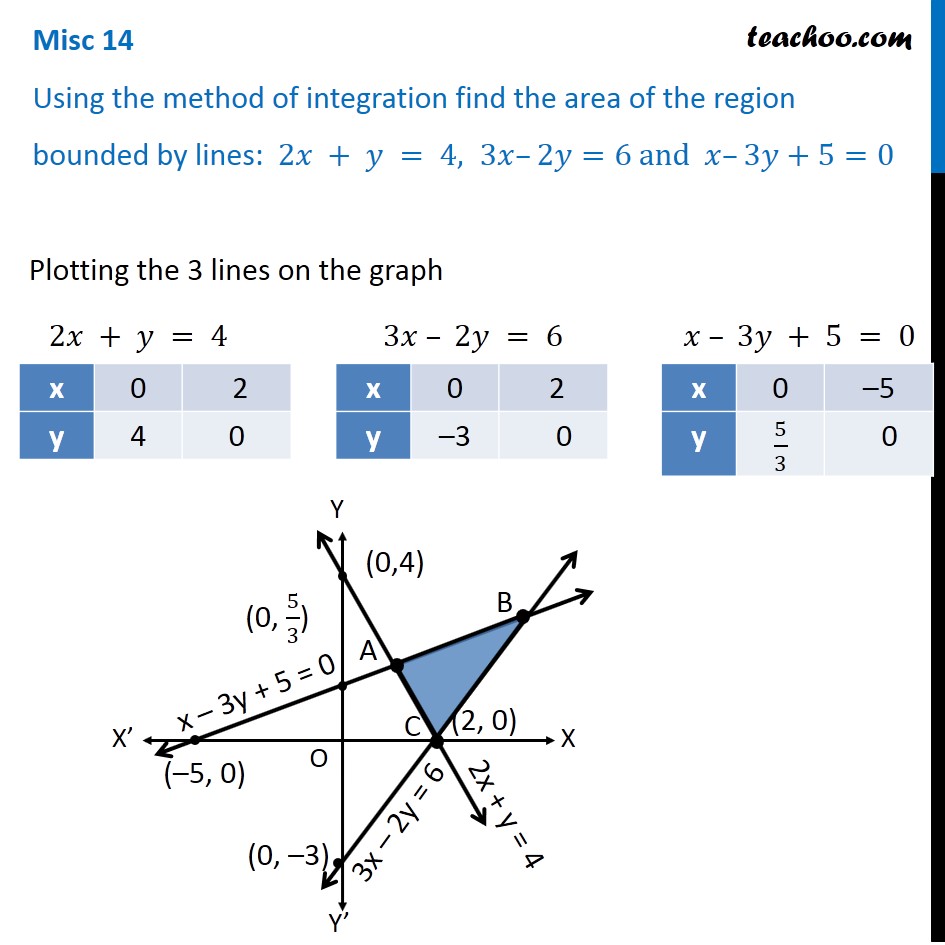



Misc 14 Find Area Bounded By Lines 2x Y 4 3x 2y 6




Draw The Graph Of Two Lines Whose Equations Are X Y 6 0 And X Y 2 0 On The Sample Graph Paper Find The Brainly In




Solve Graphically X 2y 0 3x 4y
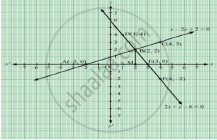



Solve Graphically The System Of Equations X 2y 2 0 2x Y 6 0 Find The Coordinates Of The Vertices Of The Triangle Formed By These Two Lines And The X Axis Mathematics Shaalaa Com




Class 10 Mathematics Chapter 3 Ncert Exemplar Solution Part Iva




Draw The Graph Of X Y 1 0 And 3x 2y 12 0 Find The Coordinates Of The Vertices Of Triangle Formed By Brainly In



What Is The Area Of The Triangle Formed By The Lines X 5 2x 3y 4 0 And X 2y 1 0 Quora
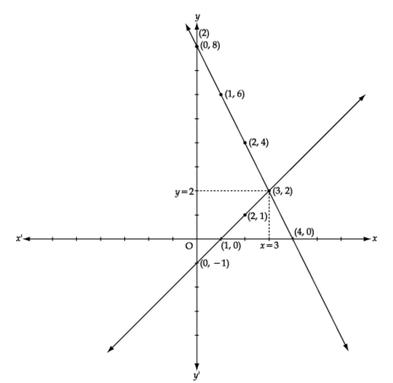



Solve X Y 1 And 2x Y 8 Graph Mathematics Topperlearning Com 4q3fx13uu
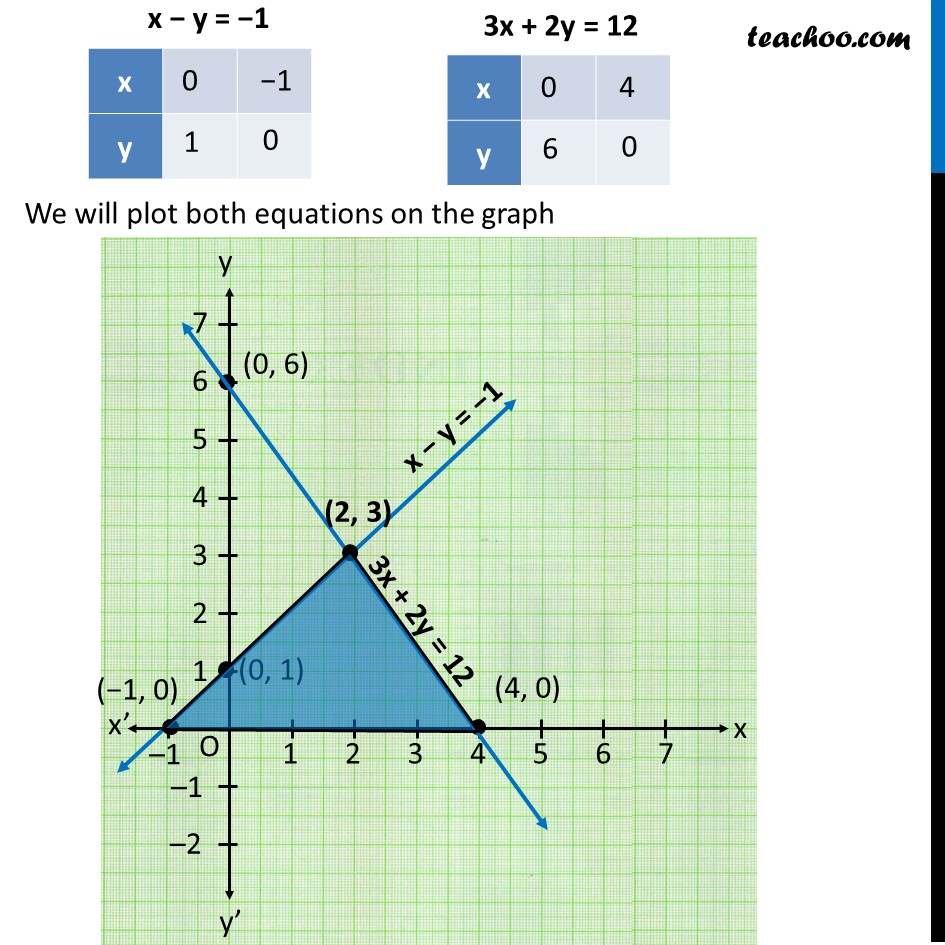



Ex 3 2 7 Draw Graphs Of X Y 1 0 And 3x 2y 12 0
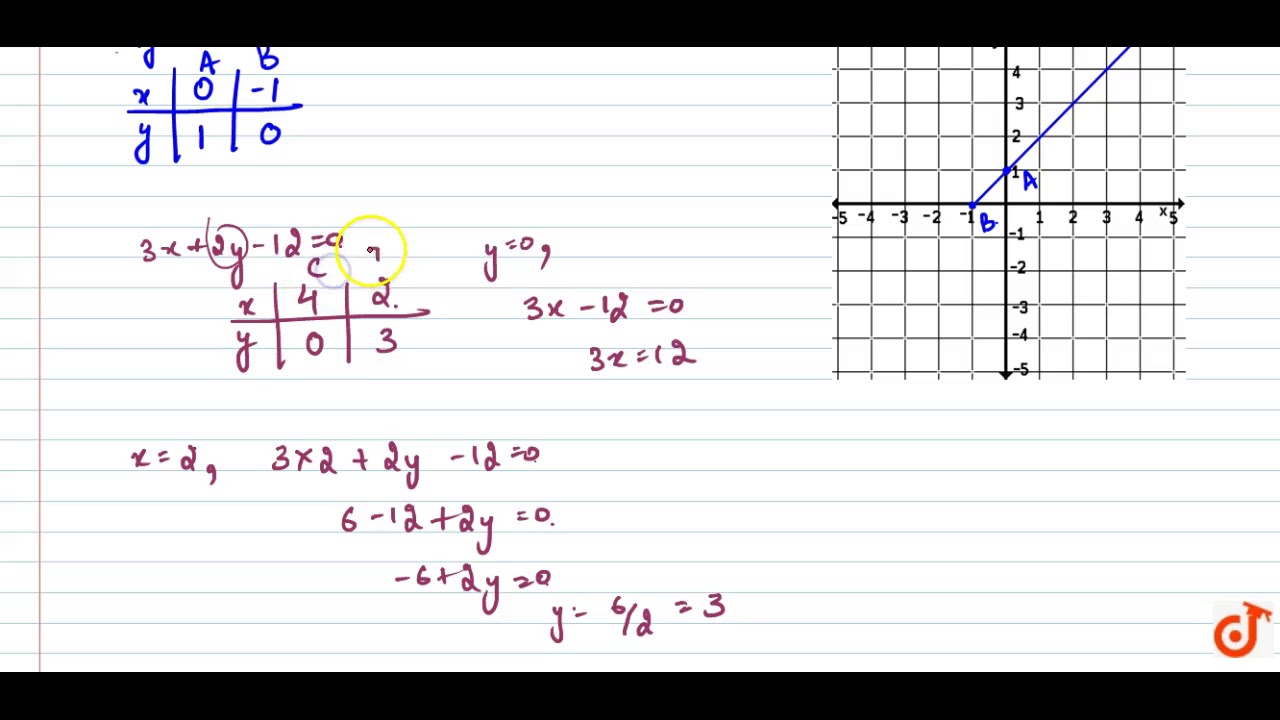



Draw The Graphs Of The Equations X Y 1 0 And 3x 2y 12 0 Determine The Coordinates Of The V Youtube




Solve Each Of The Following System Of Equations Graphically And Find The Vertices And Area Of The Triangle Formed By These Lines And The X Axis 2x 3y 4 0 X 2y 5 0



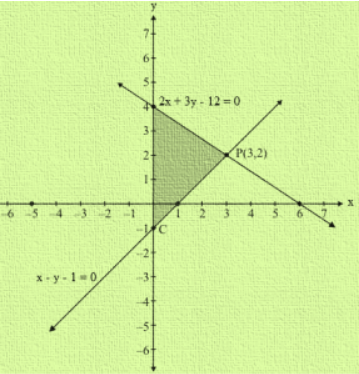
Area Of The Triangle Formed By The Lines 2x 3y 12 X Y 1 0 And X 0 Linear Equations In Two Variables Maths Class 9



R D Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2




Draw The Graphs Of The Following Linear Equations On The Same Graph Paper 2x 3y 12 X Y 1 Find Brainly In
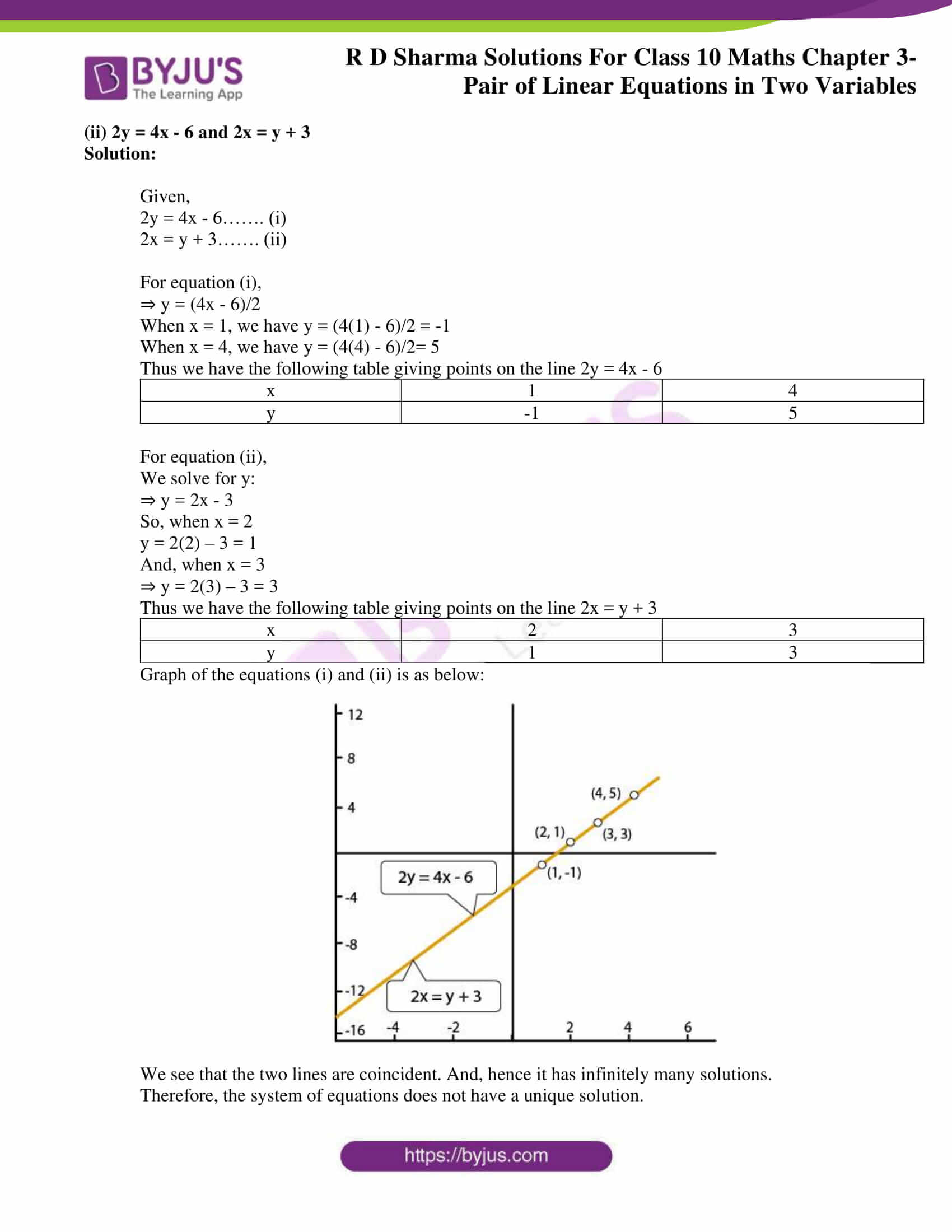



Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2




Ex 3 7 6 Optional Draw Graphs Of Equations 5x Y 5 3x Y 3



What Is The Area Of A Triangle Bounded By The Lines Y 2x Y 2x And Y 6 Quora




Draw The Graphs Of The Equations 4x Y 8 0 And 2x 3y 6 0 Also Determine The Vertices Of Brainly In



Q Tbn And9gcsvl309ow Lcvdda8 Meymt9tiqcl5z Elfgsg6bbhmbhvvbqr5 Usqp Cau



Draw The Graphs Of The Following Equations 2x Y 1 X 2y 13 Find The Solution Of The Equations From The Graph Sarthaks Econnect Largest Online Education Community
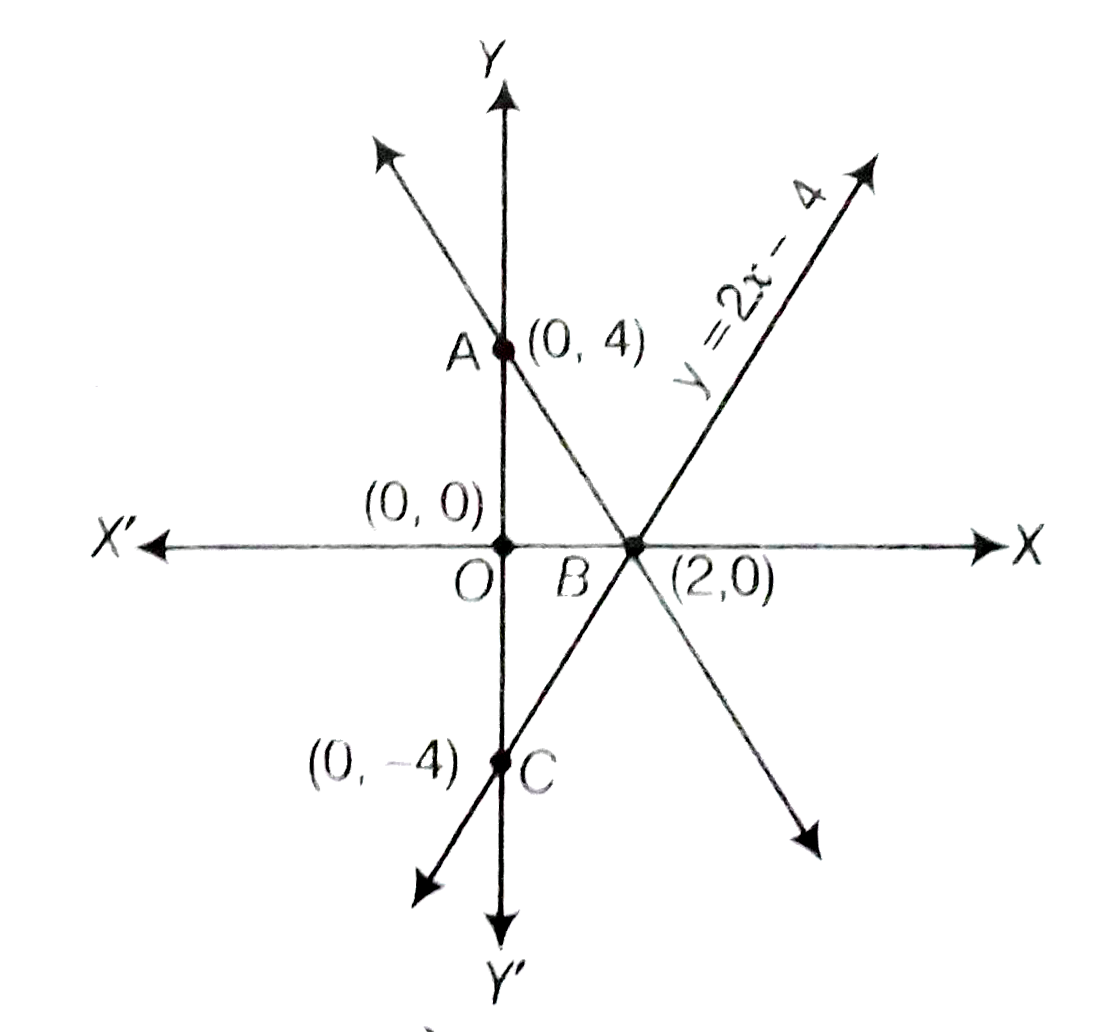



Draw The Graph Of The Pair Of Equations 2x Y 4 And 2x Y 4 Write T
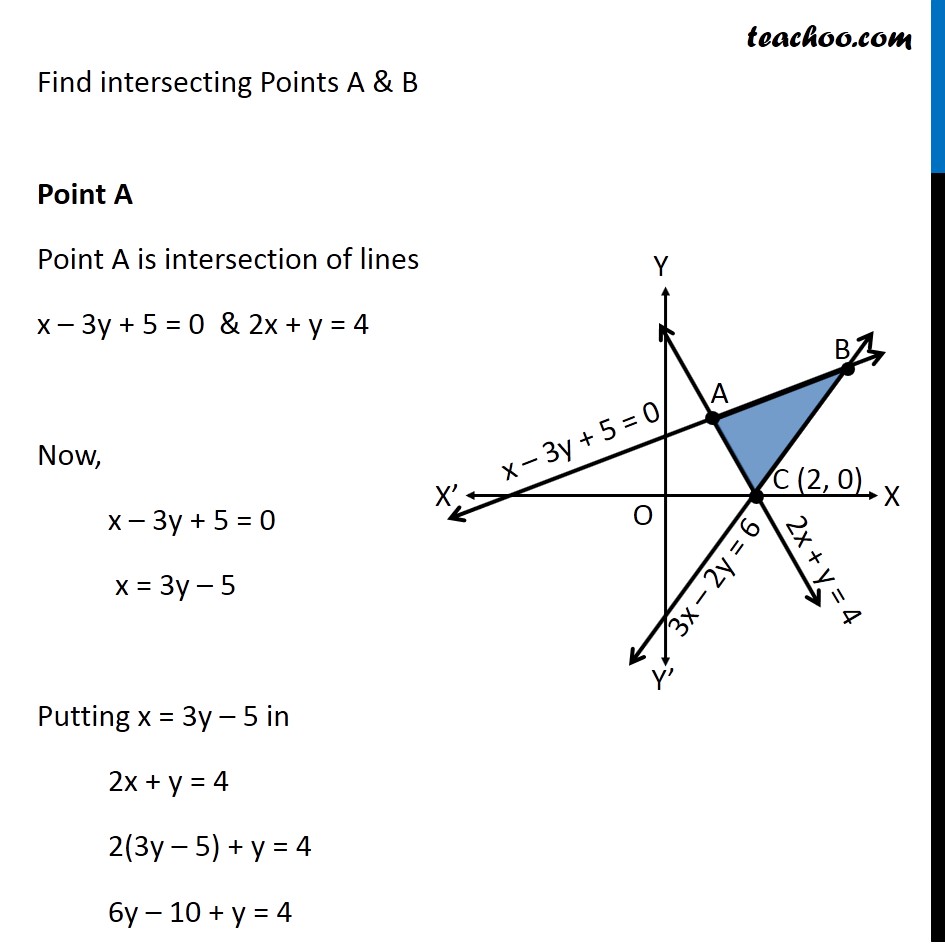



Misc 14 Find Area Bounded By Lines 2x Y 4 3x 2y 6




Solution Find The Area Of The Triangle Which The Line 2x 3y 6 0 Forms



Q Tbn And9gcql1clwan760czvp4dqdgprlq Lweykbokd1yo8ohqz9du2wn9k Usqp Cau



Draw The Graph Of The Pair Of Equations 2x Y 4 And 2x Y 4 Studyrankersonline



Draw The Graph Of 2x Y 6 And 2x Y 2 0 Shade The Region Bounded By These Lines With X Axis Find The Area Of The Shaded Region Mathematics Topperlearning Com p26nrmm




Solve The Following System Of Linear Equation Graphically 2x Y 6 0 3x 2y 12 0 Also Find The Vertices Brainly In



Www Topperlearning Com R S Aggarwal And V Aggarwal Solutions Cbse Class 10 Mathematics R S Aggarwal And V Aggarwal Mathematics X Linear Equations In Two Variables




Solve The Equations Graphically 2x Y 2 2y X 4 Also Find The Area Of A Triangle Formed By The Two Lines And The Line




Solve Each Of The Following S See How To Solve It At Qanda




Draw The Graph Of X 2y 7 0 And 2x Y 4 0 Shade The Area Bounded By There Line And Y Axis Brainly In




The Circumcentre Of The Triangle Formed By The Lines Xy 2x 2




Ex 3 A Q15 X 2y 2 0 2x Y 6 0 Solve Each Of The Following Given Systems Of
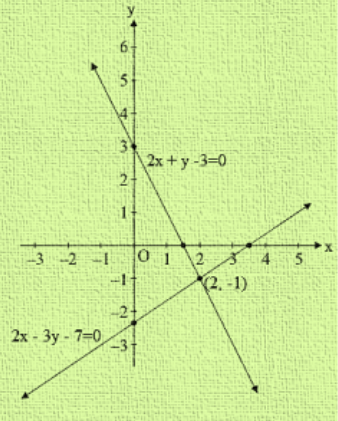



R D Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2




Solve The Following System Of Linear Equations Graphically 3x



Draw The Graphs Representing The Equations 2x Y 2 And 4x 3y 24




Solve The Following System Of Linear Equations Graphically 2x Y 6 X 2y 2 0 Find The Vertices Of The Triangle Formed By The Above Two
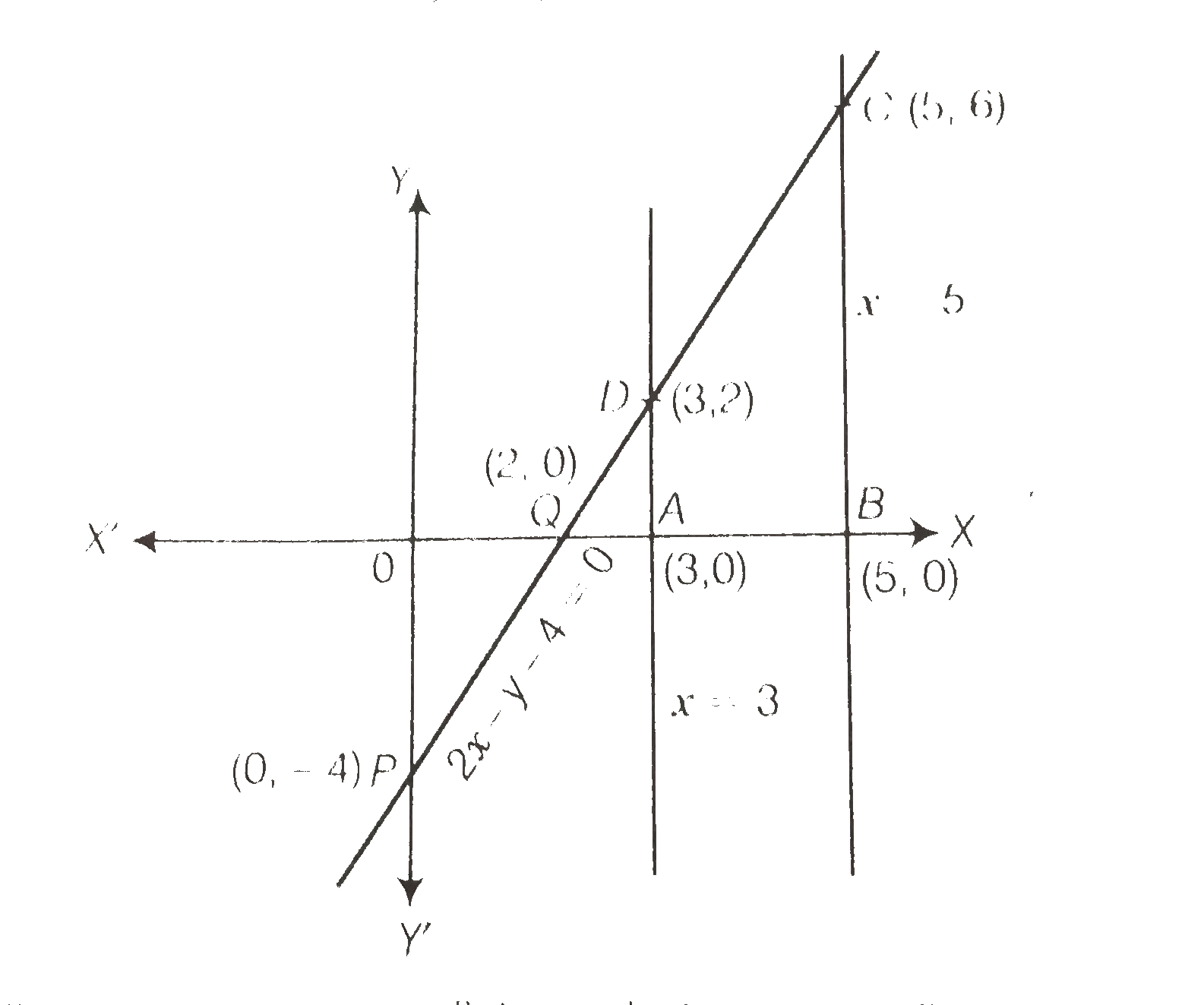



Draw The Graphs Of The Equations X 3 X 5 And 2x Y 4 0 Also Find




Draw The Graphs Of The Equations X Y 1 A N D 2x Y 8 Shade The




Draw The Graphs Of The Pair Of Linear Equations X Y 2 0 Amp 4x Y 4 0 Determine The Co Ordinates Of The Vertices Of The Triangle Formed By The Lines




The Area Of The Triangle Formed By The Coordinate Axes And The Line X Y 6 Is Square Unit Brainly In



Draw The Graph Of 2x Y 6 And 2x Y 2 0 Shade The Region Bounded By These Lines And X Axis Find The Area Of The Shaded Region Sarthaks Econnect Largest Online Education Community




How To Find Area Of Triangle Formed By A Line And Coordinate Axes Youtube


